
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)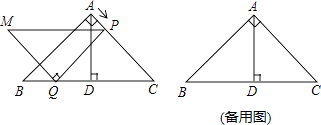
(1)当点M落在AB上时,求x的值;
(2)当点M落在AD上时,PM与CD之间的数量关系是 , 此时x的值是;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】
(1)
解:当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,
∴AP=CP=4 ![]() ,所以x=
,所以x= ![]() =4.
=4.
故答案为4.
(2)PM= ![]() CD;
CD;![]()
(3)
解:①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,
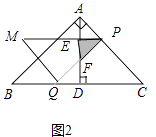
∵AP= ![]() x,
x,
∴EF=PE=x,
∴y=S△PEF= ![]() PEEF=
PEEF= ![]() x2.
x2.
②当4<x≤ ![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
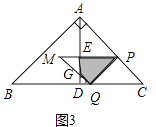
∵PQ=PC=8 ![]() ﹣
﹣ ![]() x,
x,
∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,
∴y=S△PMQ﹣S△MEG= ![]() (8
(8 ![]() ﹣
﹣ ![]() x)2﹣
x)2﹣ ![]() (16﹣3x)2=﹣
(16﹣3x)2=﹣ ![]() x2+32x﹣64.
x2+32x﹣64.
③当 ![]() <x<8时,如图4中,则重合部分为△PMQ,
<x<8时,如图4中,则重合部分为△PMQ,
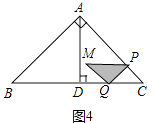
∴y=S△PMQ= ![]() PQ2=
PQ2= ![]() (8
(8 ![]() ﹣
﹣ ![]() x)2=x2﹣16x+64.
x)2=x2﹣16x+64.
综上所述y= 
【解析(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,由此即可解决问题.(2)如图1中,当点M落在AD上时,作PE⊥QC于E,先证明DQ=QE=EC,由PE∥AD,得 ![]() ,由此即可解决问题.(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤
,由此即可解决问题.(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤ ![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当 ![]() <x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
<x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
(1)求证: ![]() =
= ![]() ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕
折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的
直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸
片收展平,那么∠AFE的度数为 ( )

A. 60° B. 67.5° C. 72° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.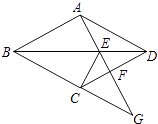
(1)求证:∠DAE=∠DCE;
(2)当CE=2EF时,EG与EF的等量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ECF=90°,线段 AB 的端点分别在 CE 和 CF 上,BD 平分∠CBA,并与∠CAB 的外角平分线 AG 所在的直线交于一点 D.
(1)∠D 与∠C 有怎样的数量关系?(直接写出关系及大小)
(2)点 A 在射线 CE 上运动,(不与点 C 重合)时,其它条件不变,(1)中结论还成立吗?说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
社会是一个重要的学校和课堂,生活是一种重要的课程和教材,实践是一种重要的学习方式和途径.参加社会生活和社会实践,不仅可以学到很多在课堂上学不到的东西,也可以把课堂上学到的理论知识同社会实践联系起来,加深对课堂学习内容的理解,我区某校七年级学生在农场进行社会实践活动时,采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:

(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
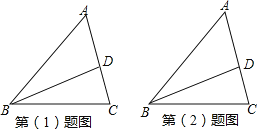
【题目】如图,已知BD为△ABC的角平分线请按如下要求操作与解答:
(1)过点D画DE∥BC交AB于点E.若∠A=68°,∠AED=42°,求△BCD各内角的度数;
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,请找出图中所有与∠A相等的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
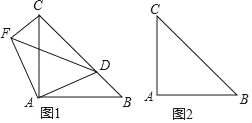
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com