
【题目】如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).
(1)求k的值;
(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围.
(3)探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由.
,并说明理由.

【答案】(1)k=![]() ;(2)△OPA的面积S=
;(2)△OPA的面积S=![]() x+18 (﹣8<x<0);(3)点P坐标为(
x+18 (﹣8<x<0);(3)点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
【解析】
(1)将点E坐标(﹣8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(﹣6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)分点P在x轴上方与下方两种情况分别求解即可得.
(1)∵直线y=kx+6过点E(﹣8,0),
∴0=﹣8k+6,
k=![]() ;
;
(2)∵点A的坐标为(﹣6,0),
∴OA=6,
∵点P(x,y)是第二象限内的直线上的一个动点,
∴△OPA的面积S=![]() ×6×(
×6×(![]() x+6)=
x+6)=![]() x+18 (﹣8<x<0);
x+18 (﹣8<x<0);
(3)设点P的坐标为(m,n),则有S△AOP=![]() ,
,
即![]() ,
,
解得:n=±![]() ,
,
当n=![]() 时,
时,![]() =
=![]() x+6,解得x=
x+6,解得x=![]() ,
,
此时点P在x轴上方,其坐标为(![]() ,
,![]() );
);
当n=-![]() 时,-
时,-![]() =
=![]() x+6,解得x=
x+6,解得x=![]() ,
,
此时点P在x轴下方,其坐标为(![]() ,
,![]() ),
),
综上,点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A的坐标为(0,﹣1),顶点B在x轴的负半轴上,顶点C在y轴的正半轴上,且∠ABC=90°,∠ACB=30°,线段OC的垂直平分线分别交OC,BC于点D,E.
(1)点C的坐标;
(2)点P为线段ED的延长线上的一点,连接PC,PA,设点P的横坐标为t,△ACP的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,点F为线段BC的延长线上一点,连接OF,若OF=CP,求∠OFP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
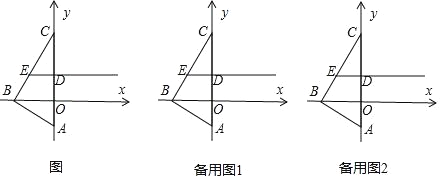
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.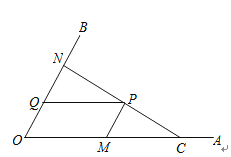
(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:![]() ﹣
﹣![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.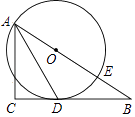
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,求x的值;
(2)当点M落在AD上时,PM与CD之间的数量关系是 , 此时x的值是;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com