
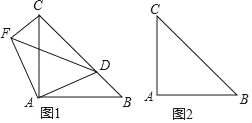
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
【答案】(1)CF=BD,且CF⊥BD,证明见解析;(2)(1)的结论仍然成立,理由见解析.
【解析】
(1)根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠BCF=90°,从而得到CF⊥BD;
(2)先求出∠CAF=∠BAD,然后与①的思路相同求解即可;
解:(1)CF=BD,且CF⊥BD,证明如下:
∵∠FAD=∠CAB=90°,
∴∠FAC=∠DAB.
在△ACF和△ABD中,
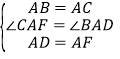 ,
,
∴△ACF≌△ABD
∴CF=BD,∠FCA=∠DBA,
∴∠FCD=∠FCA+∠ACD=∠DBA+∠ACD=90°,
∴FC⊥CB,
故CF=BD,且CF⊥BD.
(2)(1)的结论仍然成立,如图2,
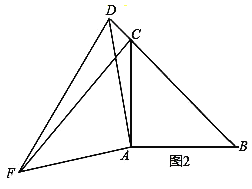
∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
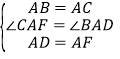 ,
,
∴△ACF≌△ABD,
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
∴CF=BD,且CF⊥BD.


科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 ![]() cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D.点P从点A出发,沿A→C方向以 ![]() cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止.在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)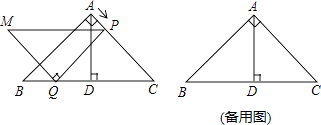
(1)当点M落在AB上时,求x的值;
(2)当点M落在AD上时,PM与CD之间的数量关系是 , 此时x的值是;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,E为OP上一点,则下列结论错误的是( )
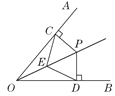
A. CE=DEB. ∠CPO=∠DEPC. ∠CEO=∠DEOD. OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正六边形ABCDEF中,N、M为边上的点,BM、AN相交于点P
(1)如图1,若点N在边BC上,点M在边DC上,BN=CM,求证:BPBM=BNBC;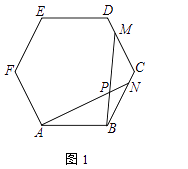
(2)如图2,若N为边DC的中点,M在边ED上,AM∥BN,求 ![]() 的值;
的值;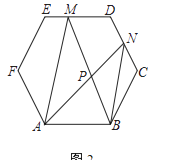
(3)如图3,若N、M分别为边BC、EF的中点,正六边形ABCDEF的边长为2,请直接写出AP的长.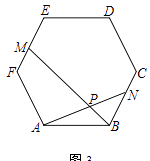
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )
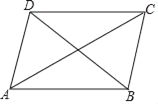
A. α B. ![]() C. 90﹣α D. 90﹣
C. 90﹣α D. 90﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是△ABC外一点,连接AD、BD、CD,若∠CDB=90°,BD=3,AD= ![]() ,则AC长为 .
,则AC长为 . 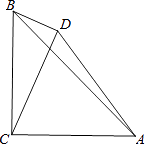
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(只保留作图痕迹)如图,在方格纸中,有两条线段AB、BC.利用方格纸完成以下操作:
(1)过点A作BC的平行线;
(2)过点C作AB的平行线,与(1)中的平行线交于点D;
(3)过点B作AB的垂线.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com