
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是△ABC外一点,连接AD、BD、CD,若∠CDB=90°,BD=3,AD= ![]() ,则AC长为 .
,则AC长为 . 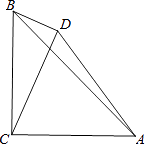
【答案】![]()
【解析】解:作AE⊥CD于E,如图所示: 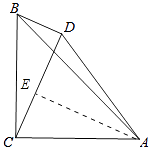
则∠AEC=∠AED=90°,
∴∠ACE+∠CAE=90°,
∵∠ACB=90°,
∴∠BCD=∠CAE,
在△ACE和△CBD中, 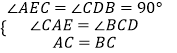 ,
,
∴△ACE≌△CBD(AAS),
∴CE=BD=3,AE=CD,
设AE=x,则DE=x﹣3,
在Rt△ADE中,AE2+DE2=AD2 ,
即x2+(x﹣3)2=( ![]() )2 ,
)2 ,
解得:x=7,或x=﹣4(舍去),
∴AE=7,
在Rt△ACE中,AC= ![]() =
= ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BD为△ABC的角平分线请按如下要求操作与解答:
(1)过点D画DE∥BC交AB于点E.若∠A=68°,∠AED=42°,求△BCD各内角的度数;
(2)画△ABC的角平分线CF交BD于点M,若∠A=60°,请找出图中所有与∠A相等的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
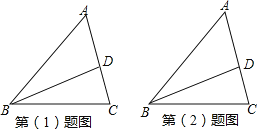
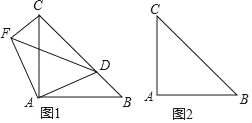
【题目】如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
(1)当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.
(2)当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD是( )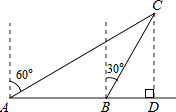
A.20海里
B.40海里
C.20 ![]() 海里
海里
D.40 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
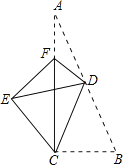
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2![]() ,BC=2,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,求折痕DF的长.
,BC=2,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,求折痕DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
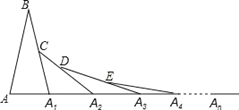
【题目】在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,第n个三角形的以An为顶点的内角的度数为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com