练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，四边形ABCD是菱形，点G是BC延长线上一点，连结AG，分别交BD、CD于点E、F，连结CE．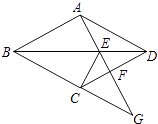

    （1）求证：∠DAE=∠DCE；
    （2）当CE=2EF时，EG与EF的等量关系是 ．

    【答案】
    （1）

    证明：∵四边形ABCD是菱形，

    ∴AD=CD，∠ADE=∠CDB；

    在△ADE和△CDE中，

    ．

    ∴△ADE≌△CDE，

    ∴∠DAE=∠DCE．


    （2）FG=3EF
    【解析】（2.）解：理由：∵四边形ABCD是菱形，
    ∴AD∥BC，
    ∴∠DAE=∠G，
    由题意知：△ADE≌△CDE
    ∴∠DAE=∠DCE，
    则∠DCE=∠G，
    ∵∠CEF=∠GEC，
    ∴△ECF∽△EGC，
    ∴ = ，
    ∵EC=2EF，
    ∴ = ，
    ∴EG=2EC=4EF，
    ∴FG=EG﹣EF=4EF﹣EF=3EF．
    故答案为FG=3EF．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数y= （x＞0）的图象经过矩形OABC对角线的交点M，分别与AB、BC相交于点D、E．，则下列结论正确的是（将正确的结论填在横线上）．
    ①s△OEB=s△ODB ， ②BD=4AD，③连接MD，S△ODM=2S△OCE ， ④连接ED，则△BED∽△BCA．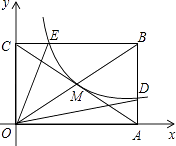

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知于点C，AC=4，BC=，将线段AC绕点A按逆时针方向旋转，得到线段AD，连接DC，DB，则线段DB的长为__________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的推理．

    如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.

    完成推理过程：

    ∵BE平分∠ABD(已知)，

    ∴∠ABD＝2∠α(__________)．

    ∵DE平分∠BDC(已知)，

    ∴∠BDC＝2∠β (__________)．

    ∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)( __________)．

    ∵∠α＋∠β＝90°(已知)，

    ∴∠ABD＋∠BDC＝180°(__________)．

    ∴AB∥CD(____________________)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：∠BAC的平分线与BC的垂直平分线DG相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3，则BE=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角三角形ABC中，∠BAC=90°，AC=8 cm，AD⊥BC于点D．点P从点A出发，沿A→C方向以 cm/s的速度运动到点C停止．在运动过程中，过点P作PQ∥AB交BC于点Q，以线段PQ为边作等腰直角三角形PQM，且∠PQM=90°（点M，C位于PQ异侧）．设点P的运动时间为x（s），△PQM与△ADC重叠部分的面积为y（cm2）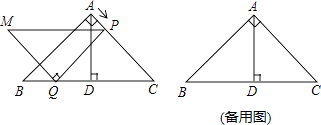

    （1）当点M落在AB上时，求x的值；
    （2）当点M落在AD上时，PM与CD之间的数量关系是 ， 此时x的值是；
    （3）求y关于x的函数解析式，并写出自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，BC＝AC，∠BCA＝90°，P 为直线 AC 上一点，过 A作 AD⊥BP 于 D，交直线 BC 于 Q．

    (1)如图 1，当 P 在线段 AC 上时，求证：BP＝AQ．

    (2)当 P 在线段 AC 的延长线上时，请在图 2 中画出图形，并求∠CPQ．

    (3)如图 3，当 P 在线段 AC 的延长线上时，∠DBA＝ 时，AQ＝2BD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAP＋∠APD＝180°，∠AOE＝∠1，∠FOP＝∠2.

    (1)若∠1＝55°，求∠2的度数；

    (2)求证：AE∥FP.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正六边形ABCDEF中，N、M为边上的点，BM、AN相交于点P

    （1）如图1，若点N在边BC上，点M在边DC上，BN=CM，求证：BPBM=BNBC；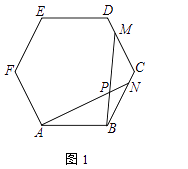

    （2）如图2，若N为边DC的中点，M在边ED上，AM∥BN，求 的值；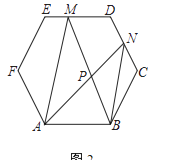

    （3）如图3，若N、M分别为边BC、EF的中点，正六边形ABCDEF的边长为2，请直接写出AP的长．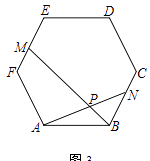

    查看答案和解析>>

    同步练习册答案