
【题目】先化简,再求值.
(1)(2x2y-4xy2)-(-![]() xy2+x2y),其中x=-1,y=2;
xy2+x2y),其中x=-1,y=2;
(2)2x2-[3(-![]() x2+
x2+![]() xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-
xy)-2y2]-2(x2-xy+2y2),其中x,y满足|x-![]() |+(y+1)2=0.
|+(y+1)2=0.
科目:初中数学 来源: 题型:
【题目】学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是全面调查 B. 样本容量是360
C. 该校只有360个家长持反对态度 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:直线l:y=﹣x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3…按此作法进行去,点A2016的坐标为( )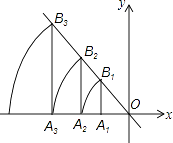
A.(﹣22016 , 0)
B.(﹣22017 , 0)
C.(﹣21008 , 0)
D.(﹣21007 , 0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 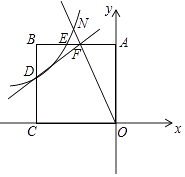
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.
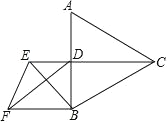
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,我们把横 、纵坐标都是整数的点叫做整点.已知点
中,我们把横 、纵坐标都是整数的点叫做整点.已知点
A(0,4),点B是![]() 轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)
轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当m=3时,点B的横坐标的所有可能值是 ▲ ;当点B的横坐标为4n(n为正整数)时,m= (用含n的代数式表示.)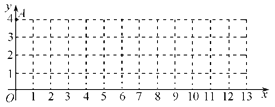
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数x、y满足2x+3y=1.
(1)用含有x的代数式表示y;
(2)若实数y满足y>1,求x的取值范围;
(3)若实数x、y满足x>﹣1,y≥﹣![]() ,且2x﹣3y=k,求k的取值范围.
,且2x﹣3y=k,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解. ∴2×(-
是方程2x3-x2+m=0的解. ∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0. ∴m=
+m=0. ∴m=![]() .
.
(1)若多项式x2+px-6分解因式的结果中有因式x-3,则实数p= ;
(2)若多项式x3+5x2+7x+q分解因式的结果中有因式x+1,求实数q的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com