
【题目】如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:OE,⑤OD2=DECD,正确的有( ) 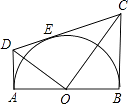
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】解:连接OE,如图所示: ∵AD与圆O相切,DC与圆O相切,BC与圆O相切,
∴∠DAO=∠DEO=∠OBC=90°,
∴DA=DE,CE=CB,AD∥BC,
∴CD=DE+EC=AD+BC,选项②正确;
在Rt△ADO和Rt△EDO中, ![]() ,
,
∴Rt△ADO≌Rt△EDO(HL),
∴∠AOD=∠EOD,
同理Rt△CEO≌Rt△CBO,
∴∠EOC=∠BOC,
又∠AOD+∠DOE+∠EOC+∠COB=180°,
∴2(∠DOE+∠EOC)=180°,
即∠DOC=90°,选项①正确;
∴∠DOC=∠DEO=90°,
又∠EDO=∠ODC,
∴△EDO∽△ODC,
∴ ![]() ,即OD2=DCDE,选项⑤正确;
,即OD2=DCDE,选项⑤正确;
∵∠AOD+∠COB=∠AOD+∠ADO=90°,
∠A=∠B=90°,
∴△AOD∽△BOC,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]() ,选项③正确;
,选项③正确;
同理△ODE∽△OEC,
∴OD:OC=DE:OE,选项④正确;
故选D.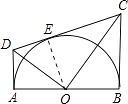
连接OE,利用切线长定理得到DE=DA,CE=CB,由CD=DE+EC,等量代换可得出CD=AD+BC,选项②正确;由AD=ED,OD为公共边,利用HL可得出直角三角形ADO与直角三角形EDO全等,可得出∠AOD=∠EOD,同理得到∠EOC=∠BOC,而这四个角之和为平角,可得出∠DOC为直角,选项①正确;由∠DOC与∠DEO都为直角,再由一对公共角相等,利用两对对应角相等的两三角形相似,可得出三角形DEO与三角形DOC相似,由相似得比例可得出OD2=DECD,选项⑤正确;由△AOD∽△BOC,可得选项③正确;由△ODE∽△OEC,可得选项④正确.


科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 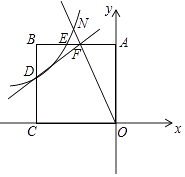
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A、B分别表示点﹣5、3,M、N两点分别从A、B同时出发以3cm/s、1cm/s的速度沿数轴向右运动.
(1)求线段AB的长;
(2)求当点M、N重合时,它们运动的时间;
(3)M、N在运动的过程中是否存在某一时刻,使BM=2BN.若存在请求出它们运动的时间,若不存在请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.下列说法:①∠BCH=∠CAE;②DF=EF;③CE=BH;④S△ABE=2S△ACE;⑤CF=![]() DF.正确的是_____.
DF.正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为( )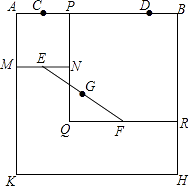
A.1
B.2
C.3
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面例题的解法,然后解答问题:
例:若多项式2x3-x2+m分解因式的结果中有因式2x+1,求实数m的值.
解:设2x3-x2+m=(2x+1)·A(A为整式).
若2x3-x2+m=(2x+1)·A=0,则2x+1=0或A=0.
由2x+1=0,解得x=-![]() .
.
∴x=-![]() 是方程2x3-x2+m=0的解. ∴2×(-
是方程2x3-x2+m=0的解. ∴2×(-![]() )3-(-
)3-(-![]() )2+m=0,即-
)2+m=0,即-![]() -
-![]() +m=0. ∴m=
+m=0. ∴m=![]() .
.
(1)若多项式x2+px-6分解因式的结果中有因式x-3,则实数p= ;
(2)若多项式x3+5x2+7x+q分解因式的结果中有因式x+1,求实数q的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是∠BCA与∠ABC的平分线的交点,过O作与BC平行的直线分别交AB、AC于D、E.已知△ABC的周长为15,BC的长为6,求△ADE的周长.
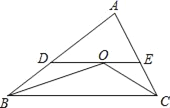
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.

证明:∵∠AGB=∠EHF(理由: )
∠AGB= (对顶角相等)
∴∠EHF=∠DGF,∴DB∥EC(理由: )
∴ =∠DBA(两直线平行,同位角相等)
又∵∠C=∠D,∴∠DBA=∠D,
∴DF∥ (内错角相等,两直线平行)
∴∠A=∠F(理由: ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com