
����Ŀ��������ѧ��չ�ԡ�����ϲ����ְҵ��Ϊ����ĵ�����Χ�ơ�����Ա����ʦ��ҽ������ʦ������Ա������ְҵ�У�����ϲ����һ�ࣿ����ѡ��ֻѡһ�ࣩ�������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ���������ͼ���ṩ����Ϣ�ش��������⣺ 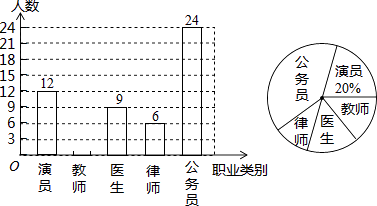
��1�����ε��鹲��ȡ�˶�����ѧ����
��2�����ڱ������ѧ���У���ϲ����ʦְҵ������������ȫ����ͳ��ͼ��
��3����������ѧ����1500��ѧ����������Ƹ���ѧ��ϲ����ʦְҵ��ѧ���ж�������
���𰸡�
��1���⣺12��20%=60��
�𣺹�������60��ѧ����
��2���⣺60��12��9��6��24=9��
����ϲ���Ľ�ʦְҵ����Ϊ9�ˣ���ͼ��ʾ�� 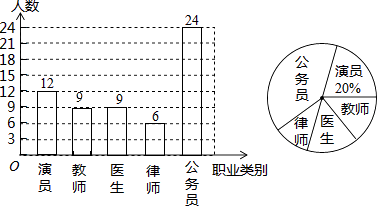
��3���⣺ ![]() ��1500=150������
��1500=150������
�𣺸���ѧ��ϲ����ʦְҵ��ѧ����150����
����������1��������ͼ����Ա�������������ͼ����Ա�İٷֱȿ�������ܵ���ѧ��������2�����ܵ�������ȥ��������ְҵ���Ϳ��Եõ���ϲ����ʦְҵ����������3�����õ���ѧ������ϲ����ʦְҵ��ѧ���ٷֱȿ��������ѧ�е���Ӧ������
�����㾫������������ͳ��ͼ������ͳ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
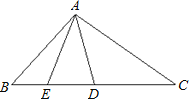
����Ŀ����֪����ͼ��D�ǡ�ABC�ı�BC�ϵ�һ�㣬��CD=AB����BDA=��BAD��AE�ǡ�ABD�����ߣ�
������B=60��,���C��ֵ��
����֤��AD�ǡ�EAC��ƽ���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
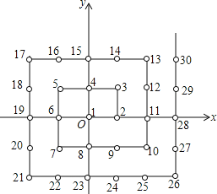
����Ŀ��ij���52��ͬѧ����У�㲥�ٱ������ųɷ��ӣ��Ȱ�ÿλͬѧ�����б�ţ�Ȼ��Ѹ��Ե�λ�ù̶���������ͼ����ƽ��ֱ������ϵ�У�ÿ����Ȼ������Ӧ��һ�����꣮����1�Ķ�Ӧ����ԭ��![]() ��3�Ķ�Ӧ����
��3�Ķ�Ӧ����![]() ��16�Ķ�Ӧ����
��16�Ķ�Ӧ����![]() ����ô���һ��ͬѧ��λ�ö�Ӧ��������____��ȫУѧ������ų�����һ���������2015��ѧ���Ķ�Ӧ���������___��
����ô���һ��ͬѧ��λ�ö�Ӧ��������____��ȫУѧ������ų�����һ���������2015��ѧ���Ķ�Ӧ���������___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���⣺
��1������ֱ���ཻ��������__________�������������__________���������ֱ�ͼ����������ͼ���еĶԶ��Ǻ��ڲ��ǵĶ�����
��2������ֱ���ཻ��������__________�������������__________���������ֱ�ͼ����������ͼ���еĶԶ��Ǻ��ڲ��ǵĶ�����
��3������������n��ֱ���ཻ��������__________�������������__________���������Զ�����__________�����ڲ�����__________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼa��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ��ʵ���ü������ֳ��Ŀ�С�����Σ�Ȼ��ͼb����״ƴ��һ�������Σ�

��1��ͼb�У��������εı߳����� ������Ӱ����С�����εı߳����� ����
��2���۲�ͼb��д����m+n��2����m��n��2��mn֮���һ��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ͰְִӼҲ���ȥ�����ְ��ȳ���һֱ����ǰ����С����������ҵ����ľ���Ϊ2500m����ͼ��С���Ͱְ�����·��s��m���벽��ʱ��t��min���ĺ���ͼ�� 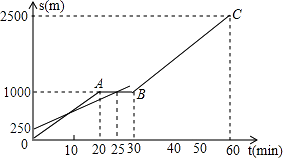
��1��ֱ��д��С������·��s��ʱ��t�ĺ�����ϵʽ��
��2��С����������ʱ����ְֵ�����������
��3�����ٶȶ����������£�С��ϣ���Ȱְ���20min���﹫����С���ڲ��й�����ͣ����ʱ�����������ĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ij�ؾ��꼶ѧ���μ�����֪ʶ�����ɼ�(��Ϊ����)�����г�ȡ��1%��ͬѧ�ľ����ɼ�����������������µ�Ƶ��ֱ��ͼ������ͼ�ν���������⣺
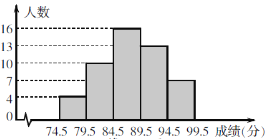
(1)��������������________________��
(2)�����ɼ���84.5��89.5����һС���Ƶ����_____________��
(3)�������ɼ���90������(��90��)��ͬѧ���Ի�ý���������Ƹõػ�ý����ľ��꼶ѧ��Լ��_____�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��DΪ��ABC��һ�㣬CDƽ����ACB��BD��CD����A=��ABD����AC=5��BC=3����BD�ij�Ϊ��������

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���BAD��������BCD��180�㩁����BDƽ����ABC��
��1����ͼ��������90�㣬���ݽ̲���һ����Ҫ����ֱ�ӿɵ� DA��CD�����������__________.
��2������������ͼ����֤AD��CD��
��3��������չ����ͼ���ڵ�����ABC�У���BAC��100�㣬BDƽ����ABC����֤��BD+AD��BC��
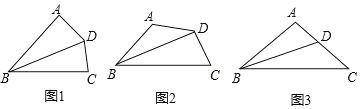
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com