
【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
科目:初中数学 来源: 题型:
【题目】数学活动课上,小敏.小颖分别画了△ABC和△DEF , 尺寸如图 . 如果两个三角形的面积分别记作S△ABC.S△DEF , 那么它们的大小关系是( )
A.S△ABC>S△DEF
B.S△ABC<S△DEF
C.S△ABC=S△DEF
D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接四边形不相邻两个顶点的线段叫做四边形的对角线,如图1,四边形ABCD中线段AC、线段BD就是四边形ABCD 的对角线.把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD的平方和与BC,AD的平方和之间的数量关系.
猜想结论:(要求用文字语言叙述)______
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梯形ABCD中AD∥BC , E是AB的中点,过E作两底的平行线交DC于F , 则下面结论错误的是( )
A.EF平分线段AC
B.梯形上下底间任意两点的连线段被EF平分
C.梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值
D.梯形EBCF的面积比梯形AEFD的面积大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC , AB=CD , ∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形,矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.设菱形相邻两个内角的度数分别为m和n , 将菱形的“接近度”定义为|m-n|,于是,|m-n|越小,菱形越接近于正方形.若菱形的一个内角为70°,则该菱形的“接近度”等于;当菱形的“接近度”等于时,菱形是正方形.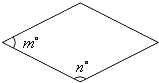
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AE⊥BC交于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′,若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( ) 
A.130°
B.150°
C.160°
D.170°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com