
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前进,小明后出发,家到公园的距离为2500m,如图是小明和爸爸所走路程s(m)与步行时间t(min)的函数图象. 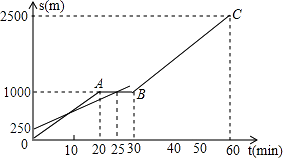
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
【答案】
(1)解:设小明所走路程s与时间t的函数关系式为s=kt+b(k≠0),
当0≤t≤20时,将点(20,1000)、(0,0)代入s=kt+b,
得: ![]() ,解得:
,解得: ![]() ,
,
∴s=50t;
当20≤t≤30时,s=1000;
当30≤t≤60时,将(30,1000)、(60,2500)代入s=kt+b,
得: ![]() ,解得:
,解得: ![]() ,
,
∴s=50t﹣500.
综上所述:小明所走路程s与时间t的函数关系式为s= 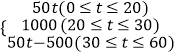
(2)解:爸爸的速度为(1000﹣250)÷25=30(m/min),
∴爸爸所走路程s与小明出发时间t的函数关系式为s=30t+250.
令s=30t+250=50t﹣500,
解得:t=37.5.
答:小明出发37.5min与爸爸第三次相遇.
(3)解:当s=30t+250=2500时,t=75,
∵75﹣60=15(min),
∴若小明比爸爸早20min到达公园,则小明在步行过程中停留的时间应缩短为5min.
【解析】(1)分0≤t≤20、20≤t≤30以及30≤t≤60三段,根据点的坐标,利用待定系数法求出函数关系式;(2)先求出爸爸所走路程s与小明出发时间t的函数关系式,再令其等于s=50t﹣500,解之即可求出二者第三次相遇的时间;(3)根据一次函数图象上点的坐标特征可求出爸爸到达公园的时间,根据它与60之间的关系,调整小明中途休息时间即可.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题: 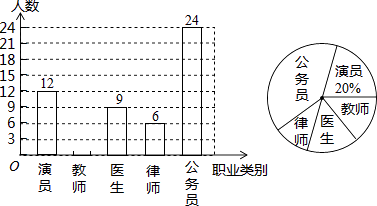
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图所示的统计图. 甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数的比为4∶17∶15,则本次测试共抽调的人数为( )
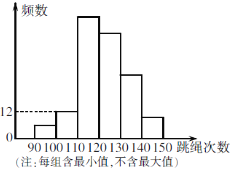
A. 120 B. 150 C. 180 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
七(3)班“绿色奥运”知识竞赛成绩频数统计表
分数段/分 | 组中值/分 | 频数/人 | 频率 |
49.5~59.5 | 54.5 | a | 0.050 |
59.5~69.5 | 64.5 | 9 | 0.225 |
69.5~79.5 | 74.5 | 10 | 0.250 |
79.5~89.5 | 84.5 | 14 | 0.350 |
89.5~99.5 | 94.5 | 5 | b |
七(3)班“绿色奥运”知识竞赛成绩频数直方图
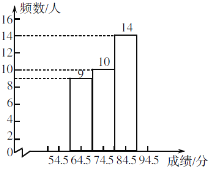
(1)频数统计表中a=_____,b=______;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点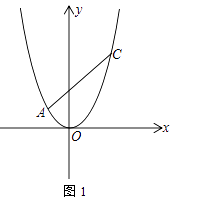
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.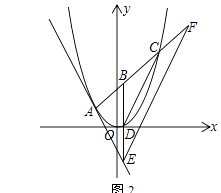
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com