
【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 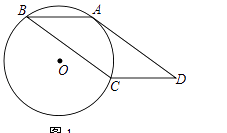
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 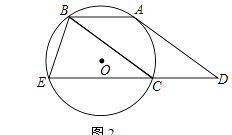
【答案】
(1)证明:证明:连接OA交BC于F.
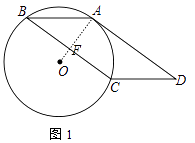
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAF=∠CFO,
∵AD是⊙O的切线,
∴∠OAD=90°,
∴∠OFC=90°,
∴OF⊥BC,
∴OA平分 ![]() ,
,
即 ![]() =
= ![]() .
.
(2)解:如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.
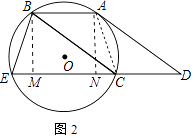
∵四边形ABCD是平行四边形,
∴∠D=∠ABC=∠BCE,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴BE=AB=AC, ![]() =
= ![]() ,
,
∴∠E=∠ACE,
在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,
,设BE=13m,则BM=12m,EM=5m,
在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,
,AC=EB=13m,则CN=5m,
∵BM=CN,BM∥CN,
∴四边形BMNA是平行四边形,
∴MN=AB=EB=13m,
∴CM=18m,
∴tan∠BCE= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠D= ![]() .
.
【解析】(1.)如图1中,连接OA交BC于F.只要证明OF⊥BC即可解决问题. (2.)如图2中,作BM⊥EC于M,AN⊥EC于N,连接AC.首先证明BE=AB=AC, ![]() =
= ![]() ,推出∠E=∠ACE,在Rt△BEM中,sin∠E=
,推出∠E=∠ACE,在Rt△BEM中,sin∠E= ![]() ,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E=
,设BE=13m,则BM=12m,EM=5m,在Rt△ANC中,sin∠ACN=sin∠E= ![]() ,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE=
,AC=EB=13m,则CN=5m,由四边形BMNA是平行四边形,推出MN=AB=EB=13m,推出CM=18m,推出tan∠BCE= ![]() =
= ![]() =
= ![]() ,可得tan∠D=
,可得tan∠D= ![]() .
.
【考点精析】掌握平行四边形的性质和切线的性质定理是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树状图或列表法中的一种列举出这辆汽车行驶方向所有可能的结果;
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某地区5000名九年级学生体育成绩状况,随机抽取了若干名学生进行测试,将成绩按A、B、C、D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题 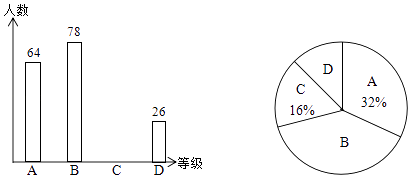
(1)在这次抽样调查中,一共抽取了名学生;
(2)请把条形统计图补充完整;
(3)请估计该地区九年级学生体育成绩为B的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
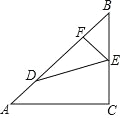
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y= ![]() x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点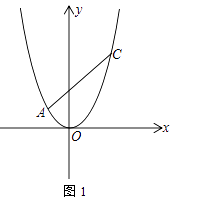
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.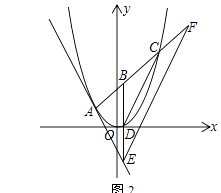
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场将一批学生书包按成本价提高50%后标价,又按标价的80%优惠卖出,每个的售价是72元.每个这种书包的成本价是多少元?利润是多少元?利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
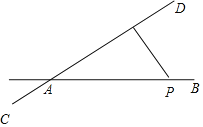
【题目】如图,有一公路AB和一铁路CD在点A处交汇,且∠BAD=30°,在公路的点P处有一所学校(学校看作点P,点P与公路AB的距离忽略不计),AP=320米,火车行驶时,火车周围200米以内会受到噪音的影响,现有一列动车在铁路CD上沿AD方向行驶,该动车车身长200米,动车的速度为180千米/时,那么在该动车行驶过程中.
(1)学校P是否会受到噪声的影响?说明理由;
(2)如果受噪声影响,那么学校P受影响的时间为多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com