
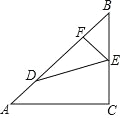
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
【答案】(1)证明见解析;(2)5.
【解析】
(1)连接 CD,利用 SAS 定理证明△ADC≌△BED,根据全等三角形的性质得到 DC=DE,∠DCA=∠EDB,根据等角的余角相等证明;
(2)作 DH⊥EC 于 H,根据等腰三角形的性质得到 EH=HC=![]() EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
解:(1)连接 CD,
∵AC=BC,∠ACB=90,
∴∠A=∠B=45°,
ADC 和△BED 中,
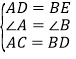
∴△ADC≌△BED(SAS),
∴DC=DE,∠DCA=∠EDB,
∴∠ECD=∠CED
∠DCA+∠ECD=∠EDB+∠FED=90°,
∴∠FED=∠ECD,
∴∠FED=∠CED;
(2)作 DH⊥EC 于 H,
∵DC=DE,DH ⊥EC,
∴EH=HC= ![]() EC,∠EDH=∠CDH,
EC,∠EDH=∠CDH,
∵DH∥AC,
∴∠CDH=∠ACD,
∴∠FDE=∠FDH,又 EF⊥AB,EH⊥DH,
∴EF=EH=![]() EC,
EC,
∵∠BFE=90°,∠B=45°,
∴EF=BF= ![]() ,
,
∴EC=5,
故答案为:5.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装厂为了估计某校七年级学生穿每种尺码校服的人数,从该校七年级学生中随机抽取了50名学生的身高数据(单位:cm),绘制成了下面的频数分布表和频数分布直方图.

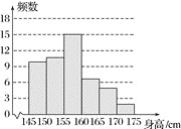
(1)表中m=________,n=________;
(2)身高x满足160≤x<170的校服记为L号,则需要订购L号校服的学生占被调查学生的百分数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
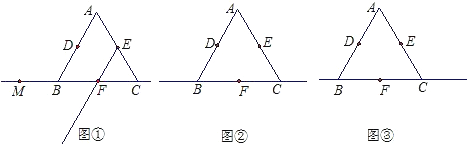
【题目】如图:已知△ABC是等边三角形,D、E、F分别是AB、AC、BC边的中点,M是直线BC上的任意一点,在射线EF上截取EN,使EN=FM,连接DM、MN、DN.
(1)如图①,当点M在点B左侧时,请你按已知要求补全图形,并判断△DMN是怎样的特殊三角形(不要求证明);
(2)请借助图②解答:当点M在线段BF上(与点B、F不重合),其它条件不变时,(1)中的结论是否依然成立?若成立,请证明;若不成立,请说明理由;
(3)请借助图③解答:当点M在射线FC上(与点F不重合),其它条件不变时,(1)中的结论是否仍然成立?不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的边AD与经过A、B、C三点的⊙O相切 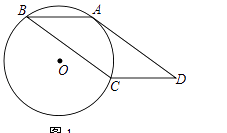
(1)求证:弧AB=弧AC
(2)如图2,延长DC交⊙O于点E,连接BE,sin∠E= ![]() ,求tan∠D
,求tan∠D 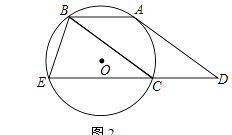
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
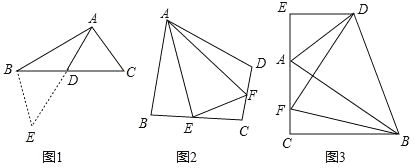
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是G,且点G在边AD上,若EG⊥AC,AB=2,则FG的长为 . 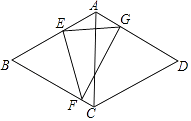
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
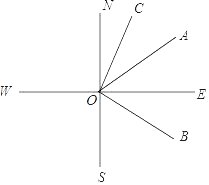
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“足球进校园”工作的推进,全国中小学生的身体素质普遍增强.某校为了准确把握学生在“足球进校园”活动开展后的体质情况,从全校学生中随机抽取部分学生进行身体素质测试,测试的结果分为A、B、C、D、E五个等级,并根据样本绘制了两幅统计图,请根据统计图的信息回答下列问题: 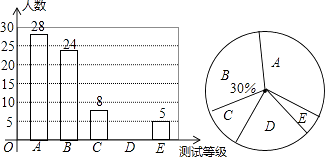
(1)本次抽样调查基抽取了学生多少人?
(2)在本次被调查的学生中,求测试结果为D等级的学生人数,并补全条形统计图.
(3)若该学校共有学生1200人,请你根据抽样调查的结果估计该学校全体学生中身体素质测试结果为A等级的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com