
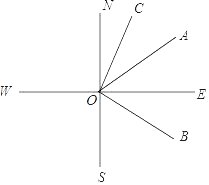
【题目】如图,直线SN⊥直线WE,垂足是点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余.
(1)写出图中与∠BOE互余的角: .
(2)若射线OA是∠BON的角平分线,探索∠BOS与∠AOC的数量关系.
【答案】(1)∠BOS,∠COE;(2)∠AOC=![]() ∠BOS.
∠BOS.
【解析】
(1)由图直接可知与∠BOE互余的角为∠BOS,∠BOS+∠CON+∠BOE+COE=180°,再由m°的角与n°的角互余可得∠BOE+∠COE=90°,据此可进行解答;
(2)由射线OA是∠BON的角平分线可得∠NOA=![]() ∠NOB,再由∠BOS与∠BON互补可求得∠NOA=
∠NOB,再由∠BOS与∠BON互补可求得∠NOA=![]() ∠BON=
∠BON=![]() (180°﹣∠BOS)=90°﹣
(180°﹣∠BOS)=90°﹣![]() ∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣
∠BOS;由∠NOC与∠BOS互余可得∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS.
∠BOS.
解:(1)首先与∠BOE互余的角有∠BOS,
由m°的角与n°的角互余知∠BOS+∠CON=90°,
∵∠BOS+∠CON+∠BOE+COE=180°,
∴∠BOE+∠COE=90°,
与∠BOE互余的角有∠BOS,∠COE,
故答案为:∠BOS,∠COE;
(2)∠AOC=![]() ∠BOS.
∠BOS.
∵射线OA是∠BON的角平分线,
∴∠NOA=![]() ∠NOB,
∠NOB,
∵∠BOS+∠BON=180°,
∴∠BON=180°﹣∠BOS,
∠NOA=![]() ∠BON=90°﹣
∠BON=90°﹣![]() ∠BOS,
∠BOS,
∵∠NOC+∠BOS=90°,∠NOC=90°﹣∠BOS,
∴∠AOC=∠NOA﹣∠NOC=90°﹣![]() ∠BOS﹣(90°﹣∠BOS)=
∠BOS﹣(90°﹣∠BOS)=![]() ∠BOS
∠BOS
∴∠AOC=![]() ∠BOS.
∠BOS.


科目:初中数学 来源: 题型:
【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3) 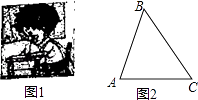
查看答案和解析>>
科目:初中数学 来源: 题型:
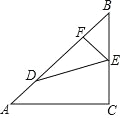
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市三景区是人们节假日游玩的热点景区,某学校对九(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下: 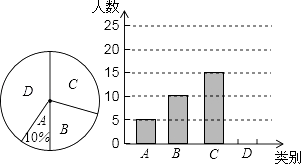
请结合图中信息解答下列问题:
(1)九(1)班现有学生人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为;
(2)请将条形统计图补充完整;
(3)若该校九年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场将一批学生书包按成本价提高50%后标价,又按标价的80%优惠卖出,每个的售价是72元.每个这种书包的成本价是多少元?利润是多少元?利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为 1,CD⊥AB 于点 D,E 为射线 CD 上一点,以BE为边在 BE 左侧作等边△BEF,则DF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
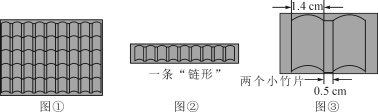
【题目】如图①是一种竹凉席,它是由规格为1.4 cm×3 cm的小竹片按横、竖方向编织而成的.如图②是这种规格的凉席横向组成部分的一条“链形”,每相邻两个小竹片的长边互相平行,且间距为0.5 cm(如图③).
(1)5个小竹片组成的“链形”长为_____cm;
(2)n个小竹片组成的“链形”长为____cm;
(3)如果此种竹凉席的长为1.99 m,那么一条“链形”中有小竹片多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
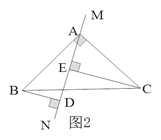
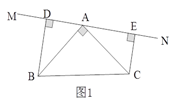
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com