
【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
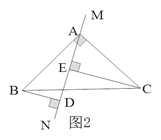
【答案】(1)DE=BD+CE,理由见解析;(2) DE= CE-BD
【解析】试题分析:(1)求出△ABD≌△CEA,根据全等三角形性质得出BD=AE,DA=CE,即可得出答案.
(2)求出△ABD≌△CAE,推出BD=AE,CE=AD,即可求出答案.
试题解析:解:(1)DE=BD+CE.理由如下:
∵BD⊥MN,CE⊥MN,∴∠BDA=∠AEC=90°,∴∠BAD+∠ABD=90°.
又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∴∠ABD=∠CAE .
在△BAD和△ACE中,∵∠BDA=∠AEC=90°,∠ABD=∠CAE,AB=CA,∴△BAD≌△ACE(AAS) ,∴BD=AE,AD=CE.
又∵DE=AE+AD,∴DE=BD+CE.
(2)DE= CE-BD.
同(1)可得△BAD≌△ACE, ∴BD=AE,AD=CE.
又DE= AD –AE,∴DE= CE-BD.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=12厘米,(即∠B=∠C),BC=9厘米,点M为AB的中点,
(1)如果点P在线段BC上以2厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1.5秒后,△BPM与△CQP是否全等?请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPM与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
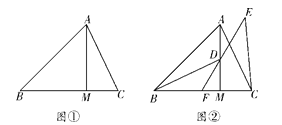
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
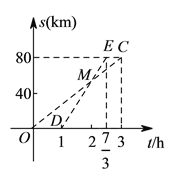
【题目】已知![]() ,
, ![]() 两地相距
两地相距![]() ,甲、乙两人沿同一公路从
,甲、乙两人沿同一公路从![]() 地出发到
地出发到![]() 地,甲骑摩托车,乙骑自行车,图中
地,甲骑摩托车,乙骑自行车,图中![]() ,
, ![]() 分别表示离开
分别表示离开![]() 地的路程
地的路程![]() 与运动时间
与运动时间![]() 的函数关系的图像.
的函数关系的图像.
(![]() )写出甲、乙的速度和点
)写出甲、乙的速度和点![]() 的坐标.
的坐标.
(![]() )若甲到达
)若甲到达![]() 地后立刻按原速度返回至
地后立刻按原速度返回至![]() 地,乙到达
地,乙到达![]() 地后停止.
地后停止.
①试求甲离开![]() 地后
地后![]() 关于
关于![]() 的函数表达式及自变量
的函数表达式及自变量![]() 的取值范围,并在直角坐标系中画出它的图像.
的取值范围,并在直角坐标系中画出它的图像.
②试求甲、乙两人再次相遇的时间![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1~4,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=-x-2交x轴于点A,交y轴于点B,抛物线y2=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)求当y1≥y2时x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com