
【题目】如图,在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分成12cm和15cm两部分,求△ABC各边的长.

【答案】AB=AC=8cm,BC=11cm或AB=AC=10cm,BC=7cm
【解析】【试题分析】本题目需要分类讨论,设AB=2xcm,BC=ycm. (1)当AB+AD=12cm,BC+CD=15cm,
列方程组得: ![]() ,解得
,解得![]() ,从而得到AB=AC=8cm,BC=11cm.
,从而得到AB=AC=8cm,BC=11cm.
(2)当AB+AD=15cm,BC+CD=12cm时,列方程组得![]() 解得
解得![]() ,AB=AC=10cm,BC=7cm.最后根据三角形的三边关系,进行验证.
,AB=AC=10cm,BC=7cm.最后根据三角形的三边关系,进行验证.
【试题解析】
设AB=2xcm,BC=ycm.有以下两种情况:(1)当AB+AD=12cm,BC+CD=15cm时, ![]() ,解得
,解得![]() 即AB=AC=8cm,BC=11cm,符合三边关系;
即AB=AC=8cm,BC=11cm,符合三边关系;
(2)当AB+AD=15cm,BC+CD=12cm时, ![]() 解得
解得![]() 即AB=AC=10cm,BC=7cm,符合三边关系.
即AB=AC=10cm,BC=7cm,符合三边关系.
综上所述,AB=AC=8cm,BC=11cm或AB=AC=10cm,BC=7cm.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】一种细胞的直径约为0.000067米,将0.000067用科学记数法表示为( )
A.6.7×105B.6.7×106C.6.7×10-5D.6.7×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1所示,等腰直角三角形ABC中,∠BAC=90O,AB=AC,直线MN经过点A,BD⊥MN于点D,CE⊥MN于点E.
(1)试判断线段DE、BD、CE之间的数量关系,并说明理由;
(2)当直线MN运动到如图2所示位置时,其余条件不变,判断线段DE、BD、CE之间的数量关系。
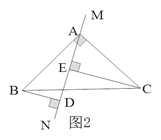
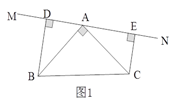
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数![]() 向上代表肉馅,点数
向上代表肉馅,点数![]() 向上代表香肠馅,点数
向上代表香肠馅,点数![]() ,
, ![]() 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.
向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.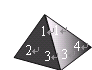
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段![]() 和射线
和射线![]() 交于点
交于点![]() .
.
(![]() )利用尺规完成以下作图,并保留作图痕迹(不写作法).
)利用尺规完成以下作图,并保留作图痕迹(不写作法).
①在射线![]() 上作一点
上作一点![]() ,使
,使![]() ,连接
,连接![]() ;
;
②作![]() 的角平分线交
的角平分线交![]() 于
于![]() 点;
点;
③在射线![]() 上作一点
上作一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(![]() )在(
)在(![]() )所作的图形中,通过观察和测量可以发现
)所作的图形中,通过观察和测量可以发现![]() ,请将下面的证明过程补充完整.
,请将下面的证明过程补充完整.

证明:∵![]() ,
,
∴![]() __________
__________![]() __________,①
__________,①
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() __________,②
__________,②
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .( )
.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
(1)利用尺规作出∠DAC的平分线AM,连接BE并延长交AM于点F,(要求在图中标明相应字母,保留作图痕迹,不写作法);
(2)试判断AF与BC有怎样的位置关系与数量关系,并说明理由.
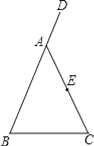
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD是BC边上的中线.
(1)画出与△ACD关于点D成中心对称的三角形;

(2)找出与AC相等的线段;
(3)探究:△ABC中AB与AC的和与中线AD之间有何大小关系?并说明理由;
(4)若AB=5,AC=3,求线段AD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
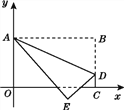
【题目】如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
(1)当m=3时,点B的坐标为_________,点E的坐标为_________;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com