
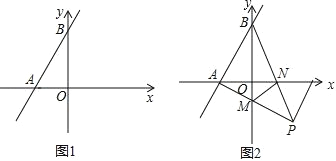
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ�� AB �ֱ� x �ᡢy ���ڵ�A��a��0���� B��0��b������a��b����a2+4a+4+|2a+b|��0
��1��a�� ��b�� ��
��2���� P ��ֱ��AB���Ҳ࣬����APB��45��
������P��x���ϣ����P������Ϊ ��
������ABP Ϊֱ�������Σ����P�����ꣻ
��2����ͼ2���ڣ�2���������£���P�ڵ������ޣ���BAP��90�㣬AP��y�ύ�ڵ�M��BP��x�ύ�ڵ�N������MN����֤��MPƽ����BMN��һ����ǣ�
���𰸡���1����2��4����2���٣�4��0������P��4��2����2����2������3���������.
��������
��1�����÷Ǹ����ĺ͵���0�����ɽ������������a��b��
��2�������õ���ֱ�������ε����ʼ��ɵó����ۣ�
�ڷ�������������õ��������ε����ʣ���ȫ�������ε��������PC��BC�����ɵó����ۣ�
��3�����жϳ���PMG=��AHP����SSS�жϳ���PMN�ա�PHN���ó���AHP=��PMN�����ɵó����ۣ�
��1����a2+4a+4+|2a+b|��0��
����a+2��2+|2a+b|��0��
��a����2��b��4��
�ʴ�Ϊ����2��4��
��2������ͼ 1���ɣ�1��֪��b��4��
��B��0��4����
��OB��4��
�� P ��ֱ�� AB ���Ҳ࣬���� x ���ϣ�
�ߡ�APB��45�㣬
��OP��OB��4��
��P��4��0����
�ʴ�Ϊ����4��0����
���ɣ�1��֪ a����2��b��4��
��A����2��0����B��0��4����
��OA��2��OB��4��
�ߡ�ABP ��ֱ�������Σ��ҡ�APB��45�㣬
��ֻ�С�ABP��90�����BAP��90�㣬
��ͼ 3��
��������ABP��90��ʱ���ߡ�APB����BAP��45�㣬
��AB��PB ��
���� P �� PC��OB �� C��
���BPC+��CBP��90�㣬
�ߡ�CBP+��ABO��90 �㣬
���ABO����BPC��
����AOB����BCP��
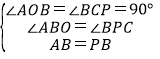
���AOB�ա�BCP��AAS����
��PC��OB��4��BC��OA��2��
��OC��OB��BC��2��
��P��4��2����
��������BAP��90��ʱ�� ���� P'�� P'D��OA �� D��
ͬ���ķ����ã���ADP'�ա�BOA��
��DP'��OA��2��AD��OB��4��
��OD��AD��OA��2��
��P'��2����2����
�������������ĵ� P��4��2����2����2����
��3����ͼ 2���ɣ�2��֪�� P��2����2����
��A����2��0����
��ֱ�� AP �Ľ���ʽΪ y����![]() x��1��
x��1��
��M��0����1����
��BM��5��
ͬ����ֱ�� BP �Ľ���ʽΪ y����3x+4��
��N��![]() ��0����
��0����
��MN��![]() ��
��
���� P �� PH��AB �� x ���� H��
�ߡ�BAP��90�㣬
���BAO+��PAH��90�㣬
���BAO+��ABM��90�㣬
���ABM����PAH��
����ABM����PAH��
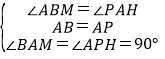 ��
��
���ABM�ա�PAH��ASA����
���AMB����PHA��AH��BM��5��
���PMG����PHA��OH��AH��OA��3��
��H��3��0����
��NH��3��![]() ��
��![]() ��MN��
��MN��
��P��2����2����M��0����1����H��3��0����
��PM��![]() ��PH��
��PH��![]() ��
��
��PM��PH��
���PNM�ա�PNH��SSS����
���AHP����PMN��
���PMG����PMN��
����MP ����BMN ��һ����ǵ�ƽ���ߣ�


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�EΪ��AB���е㣬����CBE��CE���۵õ���CFE������AF������EAF=70�㣬��ô��BCF=�ȣ� 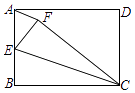
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳���һ��ѧ��������ɱ������50%���ۣ��ְ���۵�80%�Ż�������ÿ�����ۼ���72Ԫ��ÿ����������ijɱ����Ƕ���Ԫ�������Ƕ���Ԫ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
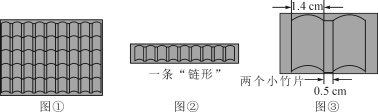
����Ŀ����ͼ����һ������ϯ�������ɹ��Ϊ1.4 cm��3 cm��С��Ƭ���ᡢ�������֯���ɵģ���ͼ�������ֹ�����ϯ������ɲ��ֵ�һ������������ÿ��������С��Ƭ�ij�����ƽ�У��Ҽ��Ϊ0.5 cm(��ͼ��)��
(1)5��С��Ƭ��ɵ�����������Ϊ_____cm��
(2)n��С��Ƭ��ɵ�����������Ϊ____cm��
(3)�����������ϯ�ij�Ϊ1.99 m����ôһ��������������С��Ƭ���ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���C=90�㣬D��AC���е㣬E��AB���е㣬��EF��BC��F���ӳ�BC��G��ʹCG=BF������CE��DE��DG��
��1����ͼ1����֤���ı���CEDG��ƽ���ı��� 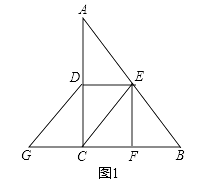 ��
��
��2����ͼ2������EG��AC�ڵ�H����EG��AB����ֱ��д��ͼ2�����г��ȵ��� ![]() GH���߶Σ�
GH���߶Σ� 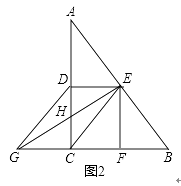
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ�ʽ�ӣ���������һЩ������ͼ�ε������

��1����ͼ1���ǽ�����������ȵ�С��������С������ƴ��һ���߳�Ϊa+b+c�������Σ����ò�ͬ�ķ����������ͼ�ε���������ܷ���ʲô���ۣ���д������
��2����ͼ2���ǽ������߳��ֱ�Ϊa��b��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�����������εı߳�����a+b=10��ab=20�����������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
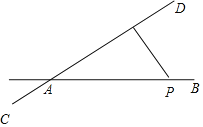
����Ŀ����ͼ����һ��·AB��һ��·CD�ڵ�A�����㣬����BAD=30�����ڹ�·�ĵ�P����һ��ѧУ��ѧУ������P����P�빫·AB�ľ�����Բ��ƣ���AP=320�ף�����ʻʱ������Χ200�����ڻ��ܵ�������Ӱ�죬����һ�ж�������·CD����AD������ʻ���ö���������200�ף��������ٶ�Ϊ180ǧ��/ʱ����ô�ڸö�����ʻ�����У�
��1��ѧУP�Ƿ���ܵ�������Ӱ�죿˵�����ɣ�
��2�����������Ӱ�죬��ôѧУP��Ӱ���ʱ��Ϊ�����룿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��2��ֱ���ཻ��1�����㣬3��ֱ���ཻ�����3�����㣬4��ֱ���ཻ�����6�����㡭�������Ĺ�����n��ֱ���ཻ���������28�������ʱn��ֵΪ��������
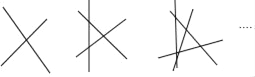
A. 18 B. 10 C. 8 D. 7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��AB��CD��OEƽ����BOC��OF��OE��OP��CD����ABO��![]() a���������н���: �١�BOE��
a���������н���: �١�BOE��![]() ��180-a��������OFƽ����BOD���ۡ�POE����BOF���ܡ�POB��2��DOF��������ȷ�ĸ����У� ������
��180-a��������OFƽ����BOD���ۡ�POE����BOF���ܡ�POB��2��DOF��������ȷ�ĸ����У� ������
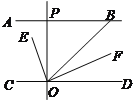
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com