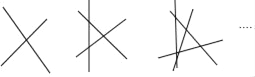
[题目]如图.2条直线相交有1个交点.3条直线相交最多有3个交点.4条直线相交最多有6个交点-按这样的规律若n条直线相交交点最多有28个.则此时n的值为( )A. 18 B. 10 C. 8 D. 7 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，2条直线相交有1个交点，3条直线相交最多有3个交点，4条直线相交最多有6个交点…按这样的规律若n条直线相交交点最多有28个，则此时n的值为（　　）

A. 18 B. 10 C. 8 D. 7

【答案】C

【解析】

由2条直线相交时最多有1个交点、3条直线相交时最多有1+2＝3个交点、4条直线相交时最多有1+2+3＝6个交点，…；可知n条直线相交，交点最多有1+2+3+…+n﹣1＝，再将28代入计算即可．

解：∵2条直线相交时，最多有1个交点；

3条直线相交时，最多有1+2＝3个交点；

4条直线相交时，最多有1+2+3＝6个交点；

…

n条直线相交，交点最多有1+2+3+…+n﹣1＝，

当＝28时，解得：n＝8或﹣7（舍）

故若有8条直线相交，最多有28个交点；

故选：C．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在菱形ABCD中，∠BAD=120°，点E、F分别在边AB、BC上，△BEF与△GEF关于直线EF对称，点B的对称点是G，且点G在边AD上，若EG⊥AC，AB=2，则FG的长为．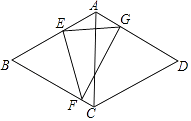

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在平面直角坐标系中，直线 AB 分别交 x 轴、y 轴于点A（a，0）点 B（0，b），且a、b满足a2+4a+4+|2a+b|＝0

（1）a＝；b＝．

（2）点 P 在直线AB的右侧，且∠APB＝45°

①若点P在x轴上，则点P的坐标为；

②若△ABP 为直角三角形，求点P的坐标；

（2）如图2，在（2）的条件下，点P在第四象限，∠BAP＝90°，AP与y轴交于点M，BP与x轴交于点N，连接MN，求证：MP平分△BMN的一个外角．

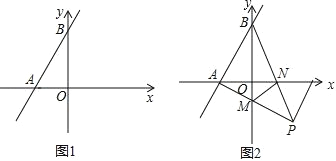
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】随着“足球进校园”工作的推进，全国中小学生的身体素质普遍增强．某校为了准确把握学生在“足球进校园”活动开展后的体质情况，从全校学生中随机抽取部分学生进行身体素质测试，测试的结果分为A、B、C、D、E五个等级，并根据样本绘制了两幅统计图，请根据统计图的信息回答下列问题：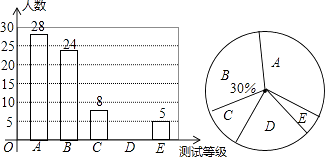
（1）本次抽样调查基抽取了学生多少人？
（2）在本次被调查的学生中，求测试结果为D等级的学生人数，并补全条形统计图．
（3）若该学校共有学生1200人，请你根据抽样调查的结果估计该学校全体学生中身体素质测试结果为A等级的学生有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，抛物线y=﹣ x2+bx+c与x轴交于点A（﹣4，0）、B（6，0）两点，与y轴交于点C．
（1）如图l，求抛物线的解析式；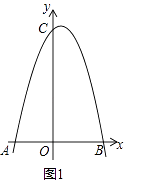

（2）如图2，点P为第一象限抛物线上一点，连接PC、PA，PA交y轴于点F，设点P的横坐标为t，△CPF的面积为S．求S与t的函数关系式（不要求写出自变量t的取值范围）；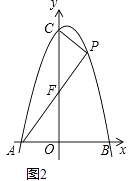

（3）如图3，在（2）的条件下，连接BC，过点P作PD∥y轴变BC于点D，点H为AF中点，且点N（0，1），连接NH、BH，将∠NHB绕点H逆时针旋转，使角的一条边H落在射线HF上，另一条边HN变抛物线于点Q，当BH=BD时，求点Q坐标．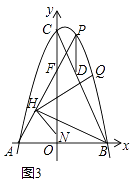

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】“绿色出行，低碳健身”已成为广大市民的共识．为方便市民出行，东台市推出了公共自行车系统，收费以小时为单位，每次使用不超过1小时的免费，超过1小时后，不足1小时的部分按1小时收费．小红同学通过调查得知，自行车使用时间为3小时，收费2元；使用时间为4小时，收费3元．她发现当使用时间超过1小时后用车费用与使用时间之间存在一次函数的关系．

（1）设使用自行车的费用为元，使用时间为小时（为大于1的整数），求与的函数解析式；