
【题目】某房产开发公司对一幢住宅楼的标价是:基价2580元/平方米,楼层差价如下表:

老王买了面积为80平方米的三楼.
(1)问老王花了多少钱?
(2)若他用同样多的钱去买六楼,请你帮老王算一算他可以多买多少平方米的房子?
【答案】(1)243552元;(2)24.9平方米
【解析】
(1)由题意知三楼每平方米的价格为:2580(1+18%)元,所以要买80平方米应花:80×2580(1+18%)元,只要设老王花了x元,列出等量关系求解即可;
(2)由题意知买六楼每平米的价格为:2580(1-10%)元,设用同样的钱买老王可以买y平方米,则多买了y-80平方米,由所用的钱相等列出等量关系求解.
(1)设老王花了x元,
由题意得:x=80×2580×(1+18%)=243552(元)
即:老王花了243552元.
(2)若他用同样多的钱去买六楼,设老王能买y平米,
由题意得:243552=y×2580×(1﹣10%),
y≈104.9平方米.
所以,若他用同样多的钱去买六楼,老王可以多买104.9﹣80=24.9平方米.


科目:初中数学 来源: 题型:
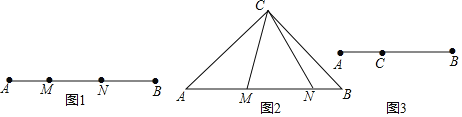
【题目】定义,如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N为线段AB的勾股分割点.
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=5,求BN的长
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点;阳阳在解决第(2)小题时遇到了困难,陈老师对阳阳说:要证明勾股分割点,则需设法构造直角三角形,你可以把△CBN绕点C逆时针旋转90度试试,请根据陈老师的提示完成证明过程.
(3)如图3,C是线段AB上的一定点,请在BC上画一点D,使C、D是线段AB的勾股分割点
(要求:完成尺规作图,保留作图痕迹,并在右侧分步写出作图步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点A(0,6)的抛物线y= ![]() x2+bx+c与x轴相交于B(﹣2,0)、C两点.
x2+bx+c与x轴相交于B(﹣2,0)、C两点.
(1)求此抛物线的函数关系式和顶点D的坐标;
(2)求直线AC所对应的函数关系式;
(3)将(1)中求得的抛物线向左平移1个单位长度,再向上平移m(m>0)个单位长度得到新抛物线y1 , 若新抛物线y1的顶点P在△ABC内,求m的取值范围;
(4)在(3)的结论下,新抛物线y1上是否存在点Q,使得△QAB是以AB为底边的等腰三角形,请分析所有可能出现的情况,并直接写出相对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
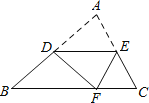
【题目】如图,在△ABC中,∠A=70°∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
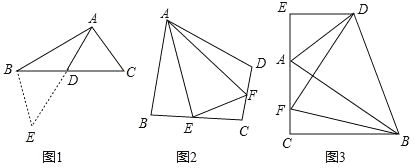
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=![]() AF.
AF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com