【题目】如图，C，D，E将线段AB分成2：3：4：5四部分，M，P，Q，N分别是AC，CD，DE，EB的中点，且MN＝21，求线段PQ的长度．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，点D为射线BC上一点，连接AD，以AD为直角边在AD的右侧作Rt△ADE，且AD=AE.
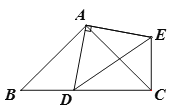
（1）填空：当点D在线段BC上时（与点B不重合），则线段CE、BD的数量关系应为________________,线段CE所在的直线与射线BC的位置关系为____________；
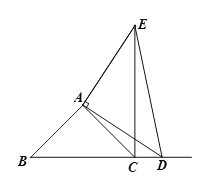
（2）如下图，当点D在线段BC的延长线上时，（1）中的结论是否仍然成立，请证明；
（3）如下图，点D在BC的延长线上，如果AC＝
cm，△CDE的面积为4cm2时，求线段DE的长度.
查看答案和解析>>
科目：初中数学 来源： 题型：
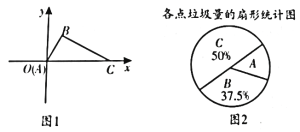
【题目】2017年4月20日，成都举行了“建城市森林，享低碳生活”的垃圾分类推进工作启动仪式，在成都设置有专门的垃圾存放点，做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示，点A在原点，
，
.某同学利用周末时间调查了这三个存放点的垃圾量，并绘制了如下尚不完整的扇形统计图（如图2）。
（1）若C处的垃圾存放量为320千克，求A处的垃圾存放量。
（2）现需要A，C两处的垃圾分别沿道路AB，CB都运到B处，若点B的横坐标为50，平面直角坐标系中一个单位长度所表示的实际距离是1米，每运送1千克垃圾1米的费用为0.005元，求本次运送垃圾的总费用。（结果保留整数，参考数据：
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一个正整数能表示成两个连续偶数的平方差，那么这个正整数为“神秘数”.
如：
因此，4，12，20这三个数都是神秘数.
（1）28和2012这两个数是不是神秘数？为什么？
（2）设两个连续偶数为
和
(其中
为非负整数)，由这两个连续偶数构造的神秘数是4的倍数，请说明理由.
（3）两个连续奇数的平方差（取正数）是不是神秘数？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某房产开发公司对一幢住宅楼的标价是：基价2580元/平方米，楼层差价如下表：
老王买了面积为80平方米的三楼．
（1）问老王花了多少钱？
（2）若他用同样多的钱去买六楼，请你帮老王算一算他可以多买多少平方米的房子？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地某月1～20日中午12时的气温(单位：℃)如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19
(1)将下列频数分布表补充完整：
气温分组(℃) | 划记 | 频数 |
12≤x＜17 |
| 3 |
17≤x＜22 | ________ | _______ |
22≤x＜27 | _________ | ________ |
27≤x＜32 |
| 2 |
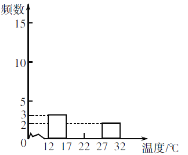
(2)补全频数分布直方图；
(3)根据频数分布表或频数分布直方图，分析数据的分布情况．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上有A，B，C，D，E五个整数点（即各点均表示整数），且AB＝2BC＝3CD＝4DE，若A、E两点表示的数的分别为－13和12，那么，该数轴上上述五个点所表示的整数中，离线段AE的中点最近的整数是（ ）
A. －1 B. 5 C. 6 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间，随机对该年级50名学生进行了调查．根据收集的数据绘制了频数分布直方图，则以下说法正确的是( )
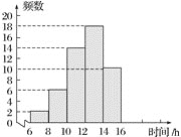
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12～14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6～8 h的大约有26人
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE，下列说法：①△ABD 和△ACD面积相等；②∠BAD＝∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE＝AE．其中正确的是（ ）
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
