
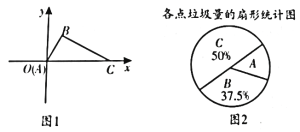
【题目】2017年4月20日,成都举行了“建城市森林,享低碳生活”的垃圾分类推进工作启动仪式,在成都设置有专门的垃圾存放点,做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示,点A在原点,![]() ,
,![]() .某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
.某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
(1)若C处的垃圾存放量为320千克,求A处的垃圾存放量。
(2)现需要A,C两处的垃圾分别沿道路AB,CB都运到B处,若点B的横坐标为50,平面直角坐标系中一个单位长度所表示的实际距离是1米,每运送1千克垃圾1米的费用为0.005元,求本次运送垃圾的总费用。(结果保留整数,参考数据:![]() )
)
科目:初中数学 来源: 题型:
【题目】如图,已知∠1和∠2互为补角,∠A=∠D.求证:AB∥CD.
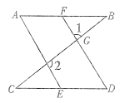
证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(______).
又∠1和∠2互为补角(已知),
∴∠CGD和∠2互为补角,
∴AE∥FD(_________),
∴∠A=∠BFD(_______).
∵∠A=∠D(已知),
∴∠BFD=∠D(_______),
AB∥CD(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= ![]() .
.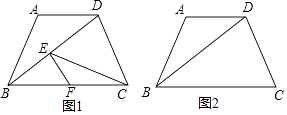
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() 则称
则称![]() 与
与![]() 是关于1的平衡数。
是关于1的平衡数。
(1)5与______是关于1的平衡数;
(2)![]() 与________是关于1的平衡数(用含
与________是关于1的平衡数(用含![]() 的代数式表示);
的代数式表示);
(3)若![]() 判断
判断![]() 与是
与是![]() 否是关于1的平衡数,并说明理由。
否是关于1的平衡数,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com