
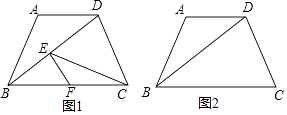
【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= ![]() .
.
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】
(1)
解:如图1,过A作AH⊥BD于H,
∵AD∥BC,AB=AD=5,
∴∠ABD=∠ADB=∠DBC,BH=HD,
在Rt△ABH中,
∵tan∠ABD=tan∠DBC= ![]() ,
,
∴cos∠ABD= ![]() ,
,
∴BH=DH=4,
∴BD=8;
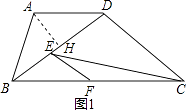
(2)
解:∵△DCE是等腰三角形,且BC=BD=8,
∴①如图2,

当CD=DE时,即:CD=DE=BD﹣BE=8﹣x,
过点D作DG⊥BC于G,
在Rt△BDG中,tan∠DBC= ![]() ,BD=8,
,BD=8,
∴DG= ![]() BD=
BD= ![]() ,BG=
,BG= ![]() BD=
BD= ![]() ,
,
∴CG=8﹣BG= ![]() ,
,
在Rt△CDG中,根据勾股定理得,DG2+CG2=CD2,
∴( ![]() )2+(
)2+( ![]() )2=(8﹣x)2,
)2=(8﹣x)2,
∴x=8+ ![]() (舍)或x=8﹣
(舍)或x=8﹣ ![]() ,
,
②如图3,
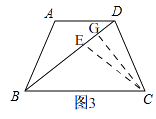
当CE=CD时,
过点C作CG⊥BD,
∴DG=EG= ![]() DE,
DE,
在Rt△BCG中,BC=8,tan∠DBC= ![]() ,
,
∴BG= ![]() ,
,
∴DG=BD﹣BG= ![]() ,
,
∴x=BE=BD﹣DE=BD﹣2DG= ![]()
(3)
解:∵BF=x,BC=10,
∴FC=10﹣x,
∴ ![]() ,
,
∵EF∥DC,
∴△FEB∽△CDB,
∴ ![]()
∴ ![]() =
= ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x(0<x<8)
x(0<x<8)
【解析】(1)过A作AH⊥BD于H,再根据AD∥BC,AB=AD=5,可得∠ABD=∠ADB=∠DBC,BH=HD,再根据tan∠ABD=tan ![]() ,计算出BH=DH=4,进而得到BD=8;(2)分两种情况用锐角三角函数计算即可得出结论.(3)首先利用平行线的性质得出△FEB∽△CDB,即可得出y与x的函数关系式;
,计算出BH=DH=4,进而得到BD=8;(2)分两种情况用锐角三角函数计算即可得出结论.(3)首先利用平行线的性质得出△FEB∽△CDB,即可得出y与x的函数关系式;
【考点精析】通过灵活运用梯形的定义和直角梯形,掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;一腰垂直于底的梯形是直角梯形即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
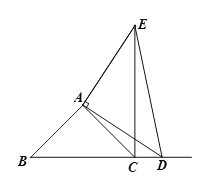
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D为射线BC上一点,连接AD,以AD为直角边在AD的右侧作Rt△ADE,且AD=AE.
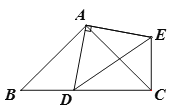
(1)填空:当点D在线段BC上时(与点B不重合),则线段CE、BD的数量关系应为________________,线段CE所在的直线与射线BC的位置关系为____________;
(2)如下图,当点D在线段BC的延长线上时,(1)中的结论是否仍然成立,请证明;
(3)如下图,点D在BC的延长线上,如果AC=![]() cm,△CDE的面积为4cm2时,求线段DE的长度.
cm,△CDE的面积为4cm2时,求线段DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行数学知识竞赛,分别设有一、二、三等奖和纪念奖,获奖情况已绘制成如图所示的两幅不完整的统计图.根据图中所给信息解答下列问题:
(1)二等奖所占的比例是多少?
(2)这次数学知识竞赛获得二等奖的有多少人?
(3)请将条形统计图补充完整.

查看答案和解析>>
科目:初中数学 来源: 题型:
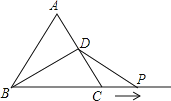
【题目】如图,等边△ABC的边长为10cm,点D是边AC的中点,动点P从点C出发,沿BC的延长线以2cm/s的速度做匀速运动,设点P的运动时间为t(秒),若△BDP是等腰三角形,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
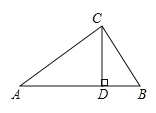
【题目】如图,∠ABD=90°,
(1)点B在直线 上,点D在直线 外;
(2)直线 与直线 相交于点A,点D是直线 与直线 的交点,也是直线 与直线 的交点,又是直线 与直线 的交点;
(3)直线 ⊥直线 ,垂足为点 ;
(4)过点D有且只有 条直线与直线AC垂直.
查看答案和解析>>
科目:初中数学 来源: 题型:
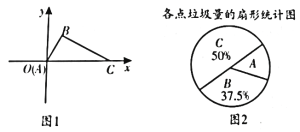
【题目】2017年4月20日,成都举行了“建城市森林,享低碳生活”的垃圾分类推进工作启动仪式,在成都设置有专门的垃圾存放点,做到日产日清。在平面直角坐标系中xOy中,A,B,C三个垃圾存放点的位置如图1所示,点A在原点,![]() ,
,![]() .某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
.某同学利用周末时间调查了这三个存放点的垃圾量,并绘制了如下尚不完整的扇形统计图(如图2)。
(1)若C处的垃圾存放量为320千克,求A处的垃圾存放量。
(2)现需要A,C两处的垃圾分别沿道路AB,CB都运到B处,若点B的横坐标为50,平面直角坐标系中一个单位长度所表示的实际距离是1米,每运送1千克垃圾1米的费用为0.005元,求本次运送垃圾的总费用。(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间,随机对该年级50名学生进行了调查.根据收集的数据绘制了频数分布直方图,则以下说法正确的是( )
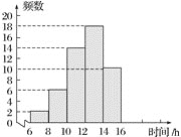
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12~14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6~8 h的大约有26人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com