
����Ŀ������֧�ִ�ѧ�����°�ʵҵ���ṩС����Ϣ���ѧ���������ܹ������ߴ���36000Ԫ���ڴ���ijƷ�Ʒ�װ���ۣ���֪�õ������Ʒ�Ʒ�װ�Ľ���Ϊÿ��40Ԫ����Ʒ�Ʒ�װ��������y�����������ۼ�x��Ԫ/����֮��Ĺ�ϵ����ͼ�е�һ���߶Σ�ʵ�ߣ�����ʾ���õ�Ӧ֧��Ա���Ĺ���Ϊÿ��ÿ��82Ԫ��ÿ�컹Ӧ֧����������Ϊ106Ԫ�������������
��1������������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��
��2�����õ��ݲ����dz��������ij������ۼ�Ϊ48Ԫ/��ʱ������������֧ƽ�⣨���۶�ɱ�=֧��������õ�Ա����������
��3�����õ�ֻ��2��Ա������õ�������Ҫ�������ܻ������д����ʱÿ����װ�ļ۸�Ӧ��Ϊ����Ԫ��

���𰸡���1��y����2x+140��
��2���õ�Ա����3�ˣ�
��3���õ�������Ҫ200���ܻ������д����ʱÿ����װ�ļ۸�Ӧ��Ϊ55Ԫ.
����������1�����ݴ���ϵ�������ɵú�������ʽ����2�������������֧�����ɵ�һԪһ�η��̣����ݽ�һԪһ�η��̣��ɵô𰸣���3�����ö��κ����ɵó�����.
�⣺��1����y��kx��b(k��0)��
�������![]() ���
���![]() ��y����2x+140��
��y����2x+140��
��2����x��48ʱ��y����2x+140��44��
��õ�Ա����a�ˣ���48��40����44��82a+106,
���a��3��
�𣺸õ�Ա����3�ˣ�
��3����ÿ�������ΪW��Ԫ���� �����⣬��
W��(x��40) y��(x��40) (��2x+140)
����2(x��55)2��450��
��������Ҫb���ܻ������д��������⣬��
450b�ݣ�82��2+106��b+36000��
���b��200��
�𣺸õ�������Ҫ200���ܻ������д����ʱÿ����װ�ļ۸�Ӧ��Ϊ55Ԫ.
���㾦�����⿴���˶��κ�����Ӧ�ã����ô���ϵ������������ʽ��һ�η��̵�Ӧ�ã�����ʽ��Ӧ�ã�����Ĺؼ��Ǹ���ͼ���������.���������е��⣬�ѶȲ�����������С��������ѵ����ڣ�3���м�ֵ����ȡ����ϣ�1���Ĺ�ϵʽ�ó�ÿ������Ķ��κ�����ת��Ϊ����ʽѰ�Ҽ�ֵ.


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д� �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥AB��ǰ����һб��CD���½ǡ�DCE=30����¥��AB=60�ף���б���µĵ�C�����¥��B������Ϊ60������б���ϵ�D�����¥��B������Ϊ45�������е�A,C,E��ͬһֱ����.
��1�����µ�C�㵽��¥����AC��ֵ��
��2�����CD�ij���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��21����2013���Ĵ���֦��8�֣�ij�ľߵ��������ף�������Ǧ�ʣ����������ֱָ�100֧������Ǧ��50֧����Ҫ1000Ԫ�����������ֱָ�50֧�����ֱָ�30֧����Ҫ550Ԫ��
��1�����ף������ֱָ�ÿ֧�������Ԫ��
��2�������ľߵ����ó�1000Ԫȫ���������������ֱָʣ����ǹ˿�����Ҫ�����иֱʵ��������������ֱָ�������6�����Ҳ��������ֱָ�������8������ô���ľߵ깲�м��ֽ���������
��3�������ľߵ�����ÿ֧���ֱָʿɻ�����2Ԫ������ÿ֧���ֱָʿɻ�����3Ԫ���ڵڣ�2���ʵĸ��ֽ��������У���һ�ַ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��AB��CD����P��������ƽ���ϣ��Ҳ���ֱ��AB��CD��AC�ϣ�����PAB=������PCD=������APC=��(��������������������180�����Ҳ�С��0��)��
��1����ͼ1������P������ƽ��ֱ��AB��CD֮�䡢ֱ��AC���ұ�ʱ��ȷ��������������������ϵ��
��2����ͼ2������P��ֱ��AB�����桢ֱ��AC���ұ�ʱ��ȷ��������������������ϵ��
��3��������������������ϵ������������ֹ�ϵ֮�⣬����������������ϵ����ֱ��д����Щ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
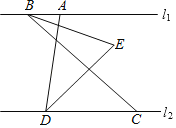
����Ŀ����ͼ����ֱ֪��l1��l2����A��B��ֱ��l1�ϣ���C��D��ֱ��l2�ϣ���C�ڵ�D���Ҳ࣬��ADC��80������ABC��n����BEƽ�֡�ABC��DEƽ�֡�ADC��ֱ��BE��DE���ڵ�E��
��1��д����EDC�Ķ���_____��
��2�������BED�Ķ������ú�n�Ĵ���ʽ��ʾ����
��3�����߶�BC����ƽ���ƶ��������������䣬��ֱ��д����BED�Ķ������ú�n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������һ���������⣺�������Ϻ���������ʵ���������º�ʮ�����º��������ʵһ�������Ϻ̶��ˡ����ϡ��º�ʵһ�˸����Σ��������ǣ�3���ϵȹ��ӽ������ʳ���ټӣ����������൱��10���µȹ��ӽ������ʳ��5���µȹ��ӽ������ʳ���ټ���һ�����൱��2���ϵȹ��ӽ������ʳ���ʣ��ϵȹ��Ӻ��µȹ���ÿ���ܽ�����ٶ���ʳ�������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά������Ȩ�棬���齨�Ĺ��Һ���ּӴ������Ϻ���Ѳ�����ȡ�һ�죬�����Һ��ബ�պ�����ij�������������ϵ�A��B����Ѳ�ߣ�ͬʱ����һ�Ҳ��������Ĵ�ֻͣ��C��������ͼ��ʾ��AB��60![]() �����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120
�����B�����C�ڱ�ƫ��45�ķ����ϣ�A�����C�ڱ�ƫ��30�ķ����ϣ��ں�����AB����һ����D�����AD��120![]() ���
���

��1���ֱ����A��C��B��C�ľ���AC��BC������������ţ�
��2����֪�ڵ���D��Χ100���ﷶΧ���а���Ⱥ������A�����ബ��ACǰ��C���̲飬;����������Σ�գ���������������������������������������������������
���ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪A��a��0����B��b��3����C��4��0���������㣨a+b��2+|a��b+6|=0���߶�AB��y����F�㣮
��1�����A��B�����ꣻ
��2����DΪy����������һ�㣬��ED��AB����AM��DM�ֱ�ƽ�֡�CAB����ODE����ͼ 2�����AMD�Ķ�����
��3����ͼ 3����Ҳ��������ͼ 1�������F�����ꣻ�����������Ƿ���ڵ�P��ʹ�á�ABP�͡�ABC�������ȣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com