
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

【答案】(1)坡底C点到大楼距离AC的值为20![]() 米;(2)斜坡CD的长度为80
米;(2)斜坡CD的长度为80![]() -120米.
-120米.
【解析】(1)在直角三角形ABC中,利用锐角三角函数定义求出AC的长即可;
(2)过点D作DF⊥AB于点F,则四边形AEDF为矩形,得AF=DE,DF=AE.利用DF=AE=AC+CE求解即可.
(1)在直角△ABC中,∠BAC=90°,∠BCA=60°,AB=60米,则AC=![]() (米)
(米)
答:坡底C点到大楼距离AC的值是20![]() 米.
米.
(2)过点D作DF⊥AB于点F,则四边形AEDF为矩形,
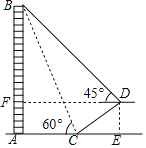
∴AF=DE,DF=AE.
设CD=x米,在Rt△CDE中,DE=![]() x米,CE=
x米,CE=![]() x米
x米
在Rt△BDF中,∠BDF=45°,
∴BF=DF=AB-AF=60-![]() x(米)
x(米)
∵DF=AE=AC+CE,
∴20![]() +
+![]() x=60-
x=60-![]() x
x
解得:x=80![]() -120(米)
-120(米)
故斜坡CD的长度为(80![]() -120)米.
-120)米.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,点E是等边△ABC的边BC上一点,以AE为边作等边△AEF,EF交AC于D.
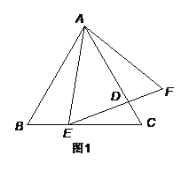
(1)连接CF,求证:![]()
(2)如图2,作EH AF交AB于点H.
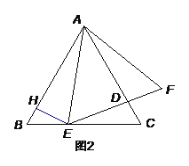
①求证:![]() ;
;
②若EH=2,ED=4,直接写出BE的长为 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
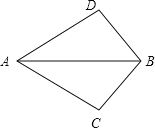
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3).
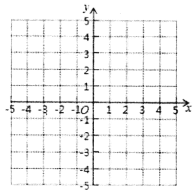
(1)直接写出△ABC 的面积为 ;
(2)在图形中作出△ABC 关于y 轴的对称图形△A1B1C1,并直接写出△A1B1C1的三个顶点的坐标:A1( ),B1( ),C1( );
(3)是否存在一点 P 到 AC、AB 的距离相等,同时到点 A、点 B 的距离也相等.若存在保留作图痕迹标出点 P 的位置,并简要说明理由;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
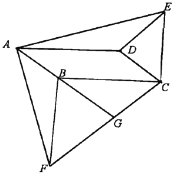
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知□ABCD中,A(1,3), B(2,-1), C(5,-5)
(1)D的坐标为____________.
(2)若经过原点的一条直线平分□ABCD的面积,求此直线的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为![]() ,宽为
,宽为![]() 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为![]() .
.
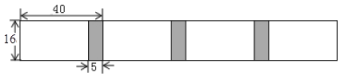
(1)根据图示,将下表补充完整;
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
(2)设![]() 张白纸粘合后的总长度为
张白纸粘合后的总长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为![]() 吗?为什么?
吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
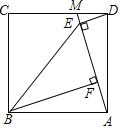
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还贷款,当某天的销售价为48元/件时,当天正好收支平衡(销售额-成本=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店至少需要多少天能还清所有贷款?此时每件服装的价格应定为多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com