
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�A��-1��5����B��-1��0����C��-4��3����
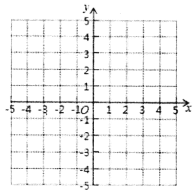
��1��ֱ��д����ABC �����Ϊ ��
��2����ͼ����������ABC ����y ��ĶԳ�ͼ�Ρ�A1B1C1����ֱ��д����A1B1C1��������������꣺A1�� ����B1�� ����C1�� ����
��3���Ƿ����һ�� P �� AC��AB �ľ�����ȣ�ͬʱ���� A���� B �ľ���Ҳ��ȣ������ڱ�����ͼ�ۼ������ P ��λ�ã�����Ҫ˵�����ɣ��������ڣ���˵�����ɣ�
���𰸡���1��7.5����2����ͼ����������1��5������1��0������4��3������3���𰸼�������
��������
��1���������������������ABC���ٸ��������ε������ʽ���ɵã�
��2���ֱ�������A��B��C����y��ĶԳƵ㣬��˳�����Ӽ��ɵã�
��3��������֪����֪��PΪ��CABƽ�������߶�AB�Ĵ�ֱƽ���ߵĽ��㣬�ݴ���ͼ�ɵã�
��1����ͼ��S��ABC![]() 5��3=7.5��
5��3=7.5��
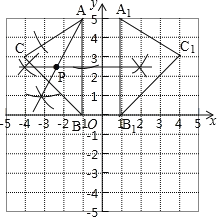
��2����ͼ��ʾ����A1B1C1��Ϊ����A1��1��5����B1��1��0����C1��4��3����
��3����ͼ��ʾ����P��Ϊ����
�ߵ�P��AC��AB�ľ�����ȣ����P�ڡ�CABƽ�����ϣ�
�ߵ���A����B�ľ���Ҳ��ȣ����P���߶�AB�Ĵ�ֱƽ�����ϣ����PΪ��CABƽ�������߶�AB�Ĵ�ֱƽ���ߵĽ��㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��B�����Ӧ�����ֱ�Ϊa��b����a��b����|a+20|=����b��13��2����C��Ӧ����Ϊ16����D��Ӧ����Ϊ��13��
��1����a��b��ֵ��
��2����A��B������ͬʱ�������������˶�����A���ٶ�Ϊ6����λ/�룬��B���ٶ�Ϊ2����λ/�룬��t��ʱ��A��ԭ��ľ���͵�B��ԭ��ľ�����ȣ���t��ֵ��
��3���ڣ�2���������£���A��B����ʼλ��ͬʱ��������A���˶�����Cʱ��Ѹ����ԭ�����ٶȷ��أ��������������۷����C�˶���B���˶���D���ֹͣ�˶�����Bֹͣ�˶�ʱ��AҲֹͣ�˶������ڴ˹����У�A��B����ͬʱ����ĵ��������϶�Ӧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
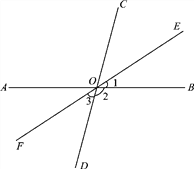
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O����BOC��80�㣬OE�ǡ�BOC�Ľ�ƽ���ߣ�OF��OE�ķ����ӳ��ߣ�
��1�����2����3�Ķ�����
��2��˵��OFƽ�֡�AOD�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC���DCE�й�������C��AB=CD��BC=CE����ABC=��DCE=90��.
��1����ͼ1������D��BC�ӳ�����ʱ.
����֤����ABC�ա�DCE.
���ж�AC��DE��λ�ù�ϵ����˵������.
��2����ͼ2����CDE�ӣ�1����λ�ÿ�ʼ�Ƶ�C˳ʱ����ת������D����BC����ʱֹͣ.
������A=60�㣬����ת�Ķ���Ϊ![]() ����
����![]() Ϊ��ֵʱ��DE���ABCһ��ƽ��.
Ϊ��ֵʱ��DE���ABCһ��ƽ��.
����ͼ3����AB=c�� BC=a�� AC=b�� a>c����BC��DE���ڵ�F���������˶������У�F��BC�ϵ��˶�·�̣��ú�a�� b�� c�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
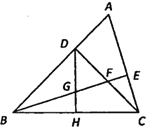
����Ŀ����ͼ������ABC�У���ABC��45�㣬CD��AB�ڵ�D��BEƽ�֡�ABC����BE��AC�ڵ�E����CD�ཻ�ڵ�F��H�DZ�BC���е㣬���� DH�� BE�ཻ�ڵ� G����GE��3����BF��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
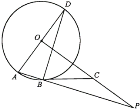
����Ŀ����ͼ��AD�ǡ�O��ֱ����ABΪ��O���ң�OP��AD��OP��AB���ӳ��߽��ڵ�P����B������߽�OP�ڵ�C.
��1����֤����CBP=��ADB.
��2����OA=2��AB=1�����߶�BP�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥AB��ǰ����һб��CD���½ǡ�DCE=30����¥��AB=60�ף���б���µĵ�C�����¥��B������Ϊ60������б���ϵ�D�����¥��B������Ϊ45�������е�A,C,E��ͬһֱ����.
��1�����µ�C�㵽��¥����AC��ֵ��
��2�����CD�ij���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=����x��h��2��hΪ�����������Ա���x��ֵ����2��x��5ʱ�������Ӧ�ĺ���ֵy�����ֵΪ��1����h��ֵΪ�� ��
A. 3��6 B. 1��6 C. 1��3 D. 4��6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com