
 ��ͼ����ƽ��ֱ������ϵ�У���������x�ύ�ڵ�A��-1��0���͵�B��1��0����ֱ��y=2x-1��y�ύ�ڵ�C���������߽��ڵ�C��D��
��ͼ����ƽ��ֱ������ϵ�У���������x�ύ�ڵ�A��-1��0���͵�B��1��0����ֱ��y=2x-1��y�ύ�ڵ�C���������߽��ڵ�C��D������ ��1�����������C���꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2������ֱ���������ߵĽ���ʽ���ⷽ��������D�����꣬�����ù��ɶ��������CD�ij���
��3������ƽ�Ƶ����ʿ�֪PQ=CD��������PQ�ij����ڡ�GPQΪ����ֱ�������Σ����������Σ��ֱ���ݵ���ֱ�������ε����ʿ����G�����꣮
��� �⣺
��1��ֱ��y=2x-1����x=0ʱ��y=-1�����C����Ϊ��0��-1����
�������߽���ʽΪy=ax2+bx+c��
�ߵ�A��-1��0����B��1��0����C��0��-1�����������ϣ�
��$\left\{\begin{array}{l}{a-b+c=0}\\{a+b+c=0}\\{c=-1}\end{array}\right.$�����$\left\{\begin{array}{l}{a=1}\\{b=0}\\{c=-1}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=x2-1��
��2������ֱ���������߽���ʽ�ɵ�$\left\{\begin{array}{l}{y=2x-1}\\{y={x}^{2}-1}\end{array}\right.$�����$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$��
��D��2��3����
��CD=$\sqrt{{2}^{2}+��3+1��^{2}}$=2$\sqrt{5}$��
��3������ƽ�Ƶ����ʿ�֪PQ=CD=2$\sqrt{5}$��
����G��0��t������GC=t+1��
��Rt��OCE�������OE=$\frac{1}{2}$��OC=1��
��CE=$\frac{\sqrt{5}}{2}$��
����GPQΪ����ֱ�������Σ��������������Σ�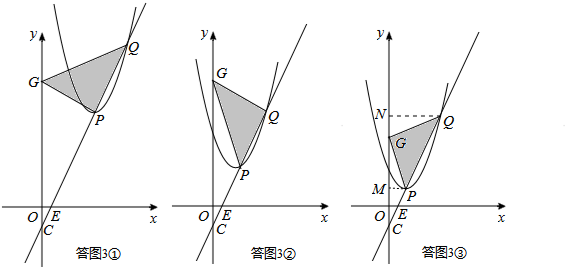
i������PΪֱ�Ƕ��㣬���ͼ3����ʾ����GP=PQ=2$\sqrt{5}$��
������ɵá�GPC�ס�EOC��
��$\frac{GP}{OE}$=$\frac{GC}{CE}$����$\frac{2\sqrt{5}}{\frac{1}{2}}$=$\frac{t+1}{\frac{\sqrt{5}}{2}}$�����t=9��
��G��0��9����
ii������QΪֱ�Ƕ��㣬���ͼ3����ʾ��
��QG=PQ=2$\sqrt{5}$��
ͬ���ɵã�G��0��9����
iii������GΪֱ�Ƕ��㣬���ͼ3����ʾ��
��ʱPQ=2$\sqrt{5}$��
��GP=GQ=$\sqrt{10}$��
�ֱ����P��Q��y��Ĵ��ߣ�����ֱ�Ϊ��M��N��
�ڡ�PMG�͡�GNQ��
$\left\{\begin{array}{l}{��PMG=��GNQ}\\{��PGM=��GQN}\\{PG=QG}\end{array}\right.$
��Rt��PMG��Rt��GNQ��AAS����
��GN=PM��GM=QN��
��Rt��QNG�У��ɹ��ɶ����ã�GN2+QN2=GQ2��
��PM2+QN2=10 ��
��C��D��������2��
���P��Q���������2��
��NQ=PM+2��
�����ʽ�ã�PM2+��PM+2��2=10��
���PM=1��
��NQ=3��
��ֱ��y=2x-1�У���x=1ʱ��y=1��
��P��1��1����
��OM=1��
��OG=OM+GM=OM+NQ=1+3=4��
��G��0��4����
�������������������ĵ�G��������������Ϊ��0��4����0��9����
���� �����Ƕ��κ���ѹ���⣬�漰�����ڶ࣬��Ҫ����������㣮�ڣ�3�����У�G��P��Q�����Ϊ���㣬ʹ�ý����Ѷ�������������߶�PQ�ij����ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2 | B�� | 1��3 | C�� | 2��3 | D�� | 3��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��ʱ�䣨Сʱ�� | 3 | 3.5 | 4 | 4.5 |
| ���� | 1 | 1 | 2 | 1 |
| A�� | ��λ����4��ƽ������3.75 | B�� | ������4��ƽ������3.75 | ||
| C�� | ��λ����4��ƽ������3.8 | D�� | ������2��ƽ������3.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
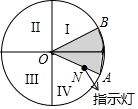 ��ͼ��ʾ����һ��Բ���ĵȷ֣������ĸ�����ֱ���Ϣ���ֻ�������Ϊ��Ӧ�������Ľ�Ϊ55�������AOB�Ƶ�0ת��������뾶OA��װ�д�ָʾ�Ƶĸ�Ӧװ�ã�������AOB������I���ص���ԭ����⣩�IJ���ʱ��ָʾ�ƻᷢ�⣬�����⣬������AOB����ת��ʱ��ָʾ�Ʒ���ĸ���Ϊ��������
��ͼ��ʾ����һ��Բ���ĵȷ֣������ĸ�����ֱ���Ϣ���ֻ�������Ϊ��Ӧ�������Ľ�Ϊ55�������AOB�Ƶ�0ת��������뾶OA��װ�д�ָʾ�Ƶĸ�Ӧװ�ã�������AOB������I���ص���ԭ����⣩�IJ���ʱ��ָʾ�ƻᷢ�⣬�����⣬������AOB����ת��ʱ��ָʾ�Ʒ���ĸ���Ϊ��������| A�� | $\frac{1}{6}$ | B�� | $\frac{7}{12}$ | C�� | $\frac{5}{12}$ | D�� | $\frac{5}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [��+6$\frac{1}{3}$��+��+4$\frac{2}{3}$��+18]+[��-18��+��-6.8��+��-3.2��] | B�� | [��+6$\frac{1}{3}$��+��-6.8��+��+4$\frac{2}{3}$��]+[��-18��+18+��-3.2��] | ||
| C�� | [��+6$\frac{1}{3}$��+��-18��]+[��+4$\frac{2}{3}$��+��-6.8��]+[18+��-3.2��] | D�� | [��+6$\frac{1}{3}$��+��+4$\frac{2}{3}$��]+[��-18��+18]+[��-3.2��+��-6.8��] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 8 | C�� | 10 | D�� | 8��10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com