
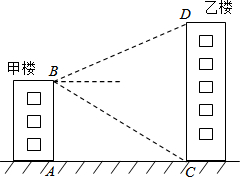
 如图,甲、乙两楼的距离AC=30m,甲楼高AB=40m,自甲楼楼顶的B处看乙楼楼顶的D处,仰角为28°,求乙楼的高CD的长.(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
如图,甲、乙两楼的距离AC=30m,甲楼高AB=40m,自甲楼楼顶的B处看乙楼楼顶的D处,仰角为28°,求乙楼的高CD的长.(结果精确到0.1m,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)  学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
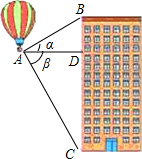 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.
如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球与楼的水平距离AD为100米,试求这栋楼的高度BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是(2,0)或(4,0).
如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是(2,0)或(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | B. | $\frac{{x}^{2}+2x+1}{x+1}$ | C. | $\frac{2ax}{3ay}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10(1+x)2=16.9 | B. | 10(1+2x)=16.9 | C. | 10(1-x)2=16.9 | D. | 10(1-2x)=16.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com