
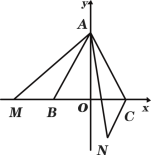
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У��ȱߡ�ABC�ı�BC��x���ϣ�A��0��3����B��![]() ��0������M��
��0������M��![]() ��0��Ϊx���ϵ�һ�����㣬����AM����AM�Ƶ�A��ʱ����ת60���õ�AN��
��0��Ϊx���ϵ�һ�����㣬����AM����AM�Ƶ�A��ʱ����ת60���õ�AN��
(1)��M����B�����ʱ������CN����֤����BAM�ա�CAN��
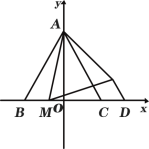
(2)��ͼ2����M���ڱ�BC��ʱ������N��ND//AC��x���ڵ�D������MN����![]() ������D������ꣻ
������D������ꣻ
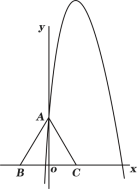
(3)��ͼ3���Ƿ���ڵ�M��ʹ�õ�Nǡ����������![]() �ϣ�������ڣ������m��ֵ����������ڣ���˵�����ɣ�
�ϣ�������ڣ������m��ֵ����������ڣ���˵�����ɣ�
���𰸡�(1)��������(2)D(![]() ��0)��(3)���ڣ�
��0)��(3)���ڣ�![]() ��
��![]()
��������
��1�����ݵȱ������ε����ʡ���ת�����ʡ��ǵĺͲ�ɵ�![]() ��
��![]() ��
��![]() ���ٸ���ȫ�������ε��ж����ɵ�֤���ۣ�
���ٸ���ȫ�������ε��ж����ɵ�֤���ۣ�
��2����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ���ɵó�
���ɵó�![]() �ǵȱ������Σ��ٽ����֪�������ݵȱ������ε����ʡ���
�ǵȱ������Σ��ٽ����֪�������ݵȱ������ε����ʡ���![]() �ǵ�ֱ�������ε����ʵȿ��г�����
�ǵ�ֱ�������ε����ʵȿ��г�����![]() �ķ��̣����
�ķ��̣����![]() ������ô𰸣�
������ô𰸣�
��3���ɣ�2����֪��![]() ������Ϊ
������Ϊ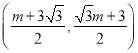 ������
������![]() ��������������߽���ʽ�ⷽ�̼��ɵý⣮
��������������߽���ʽ�ⷽ�̼��ɵý⣮
�⣺��1��֤������![]() �ǵȱ�������
�ǵȱ�������
��![]() ��
��![]()
�߽�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() �õ�
�õ�![]()
��![]() ��
��![]()
��![]()
��![]()
����![]() ��
��![]() ��
��
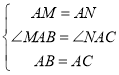
��![]() ��
��
��2����![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��
��![]() �ӳ����ڵ�
�ӳ����ڵ�![]() ����ͼ��
����ͼ��

���ɣ�1����֪![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() �ǵȱ�������
�ǵȱ�������
��![]()
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��
��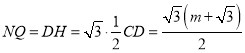
��![]()
��![]()
��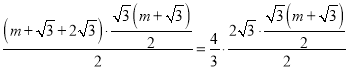
��![]()
��![]()
��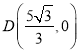 ��
��
��3���ɣ�2����֪��![]() ������Ϊ
������Ϊ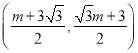
������![]() ǡ����������
ǡ����������![]() ��
��
��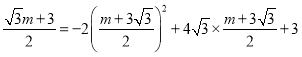
��![]() ��
��![]()
����ڵ�![]() ��ʹ�õ�
��ʹ�õ�![]() ǡ����������
ǡ����������![]() �ϣ���ʱ
�ϣ���ʱ![]() ��
��![]() ��
��


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�У�AB�ǡ�O��ֱ����GΪ��AE���е㣬����OG���ӳ�����O�ڵ�D������BD��AE�ڵ�F���ӳ�AE����C��ʹ��FC=BC������BC��
(1)��֤��BC�ǡ�O�����ߣ�
(2)��O�İ뾶Ϊ5��tanA=![]() ����FD�ij���
����FD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�����������ڣ������Ϊ10Ԫ/���ij��ˮ�����������ν��ۺ�ļ۸�Ϊ8.1Ԫ/��������ν��۵İٷ�����ͬ��
��1�������ˮ��ÿ�ν��۵İٷ��ʣ�
��2���ӵ�һ�ν��۵ĵ�1�����𣬵�x�죨xΪ���������ۼۡ��������������ķ��õ������Ϣ�����ʾ����֪����ˮ���Ľ���Ϊ4.1Ԫ/������۸�ˮ����x���죩������Ϊy��Ԫ������y��x��1��x��15��֮��ĺ�����ϵʽ��������ڼ���ʱ�����������
ʱ��x���죩 | 1��x��9 | 9��x��15 | x��15 |
�ۼۣ�Ԫ/� | ��1�ν��ۺ�ļ۸� | ��2�ν��ۺ�ļ۸� | |
������� | 80��3x | 120��x | |
�������ķ��ã�Ԫ�� | 40+3x | 3x2��64x+400 | |
��3���ڣ�2���������£���Ҫʹ��15�������ȣ�2����������������127.5Ԫ�����15���ڵ�14��ļ۸���������ɽ�����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
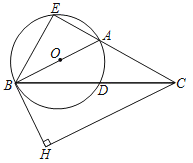
����Ŀ����ͼ������ABC�У�AB��AC����ABΪֱ���ġ�O��BC�ڵ�D���ӳ�CA����O�ڵ�E��BH�ǡ�O�����ߣ���CH��BH������ΪH��
��1����֤��BE��BH��
��2����AB��5��tan��CBE��2����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
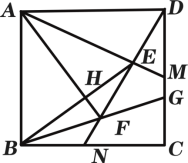
����Ŀ����ͼ����������ABCD�У�AB=2��MΪCD���е㣬NΪBC���е㣬����AM��DN���ڵ�E������BE����AH��BE�ڵ�H���ӳ�AH��DN���ڵ�F������BF���ӳ���CD���ڵ�G����MG�ij���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����9��������ͼ�ķ����У���OAB�Ķ�������ֱ�ΪO��0��0����A����2����1����B����1����3������O1A1B1����OAB�ǹ��ڵ�PΪλ�����ĵ�λ��ͼ����

��1����ͼ�б��λ������P��λ�ã���д��������꼰��O1A1B1����OAB�����Ʊȣ�
��2����ԭ��OΪλ�����ģ���y���������OAB��һ��λ����OA2B2��ʹ������OAB��λ�Ʊ�Ϊ2��1����д����B�Ķ�Ӧ��B2�����ꣻ
��3������2�������£�����M��a��b������OAB����һ�������붥���غ�����д��M����OA2B2�еĶ�Ӧ��M2��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ֪��![]() �ֱ�Ϊx�ᣬy���ཻ��A��B���㣬��P(0��m)��y����һ�����㣬���Ե�PΪԲ�ĵ�ԲP��x���ֱ��l�����У���m��ֵ��_______��
�ֱ�Ϊx�ᣬy���ཻ��A��B���㣬��P(0��m)��y����һ�����㣬���Ե�PΪԲ�ĵ�ԲP��x���ֱ��l�����У���m��ֵ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ��������ͬһ����·�ϣ�������ʻ��������У�����������ʱֹͣ.�׳���ʻһ��ʱ������ͣ��0.5Сʱ�����Ͻ��������ԭ����B����ʻ������֮���·��y��ǧ�ף������������ʱ��x(Сʱ��֮��ĺ�����ϵ��ͼ��ʾ.

��1����ס���������ʻ���ٶ�V����V��.
��2����m��ֵ.
��3�����׳�û�й���ͣ�����������ǰ�ʱ����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ڼ䣮ijС����������������A��B���ֿ��֣�������С���������Ҫ��������A�ֿ���9����B�ֿ���4��������Ҫ700Ԫ��������A�ֿ���3����B�ֿ���5��������Ҫ380Ԫ��
��1��������A��B���ֿ���ÿ����������Ԫ��
��2�������������������ֿ��ֹ�90��������A�ֿ��ְ���������B�ֿ��ְ�����2��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com