
【题目】如图,在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,连接AM和DN交于点E,连接BE,作AH⊥BE于点H,延长AH与DN交于点F.连接BF并延长与CD交于点G,则MG的长度为__________.
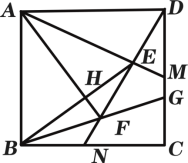
【答案】![]()
【解析】
要求MG的长度,需要先求出CG的长,过F作PQ‖BC,连接MF,设出MQ,根据三角形相似分别表示出AP,PF,QF的长,根据勾股定理求出MQ的长,再根据△FGQ![]() △BGC求出CG的长即可求MG的长.
△BGC求出CG的长即可求MG的长.
如图:
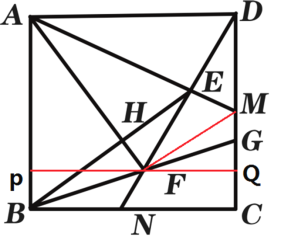
过点F作PQ平行于BC,分别交AB,DC于点P,点Q,连接MF;
∴∠APF=∠MQF=90°,
设MQ=x,则QD=x+1=AP,
∵在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,
∴MD=NC=![]() AB=1,
AB=1,
又AD=CD,
∴△AMD![]() △DNC,
△DNC,
∴∠NDC=∠DAM,
∴∠DEM=90°,
又∠MDE=∠FDQ,
∴△DEM![]() △FDQ,
△FDQ,
∴![]() ,
,
又∵∠DEM=90°,∠MDE=∠NDC,
∴△DEM![]() △DNC,
△DNC,
∴![]() ,
,
∴DE=2ME,
∵DM=1,由勾股定理可得:ME=![]() ,DE=
,DE= ![]() ,代入
,代入![]() ,
,
∴DQ=2QF,
∴QF=![]() ,
,
∴PF=2-QF= 2-![]() =
=![]() ,
,
在Rt△AMD中,AD=2,DM=1,
∴AM=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
整理得:![]() ,
,
解得:x=![]() ,x=-1(舍去),
,x=-1(舍去),
又∠FGQ=∠BGC,∠C=∠C,
∴△FGQ![]() △BGC,
△BGC,
∴![]() 即
即![]() ,
,
∵QC=CD-DQ=1-x,
∴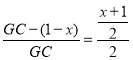 ,
,
解得:GC=![]() ,
,
∴MG=MC-GC=1-![]() =
=![]() ,
,
故答案为:![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
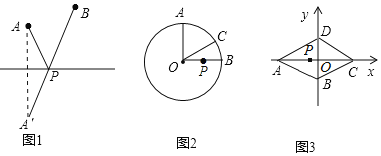
【题目】阅读材料:“最值问题”是数学中的一类较具挑战性的问题.其实,数学史上也有不少相关的故事,如下即为其中较为经典的一则:海伦是古希腊精通数学、物理的学者,相传有位将军曾向他请教一个问题﹣﹣如图1,从A点出发,到笔直的河岸l去饮马,然后再去B地,走什么样的路线最短呢?海伦轻松地给出了答案:作点A关于直线l的对称点A′,连接A′B交l于点P,则PA+PB=A′B 的值最小.
解答问题:
(1)如图2,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,求PA+PC的最小值;
(2)如图3,已知菱形ABCD的边长为6,∠DAB=60°.将此菱形放置于平面直角坐标系中,各顶点恰好在坐标轴上.现有一动点P从点A出发,以每秒2个单位的速度,沿A→C的方向,向点C运动.当到达点C后,立即以相同的速度返回,返回途中,当运动到x轴上某一点M时,立即以每秒1个单位的速度,沿M→B的方向,向点B运动.当到达点B时,整个运动停止.
①为使点P能在最短的时间内到达点B处,则点M的位置应如何确定?
②在①的条件下,设点P的运动时间为t(s),△PAB的面积为S,在整个运动过程中,试求S与t之间的函数关系式,并指出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
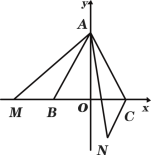
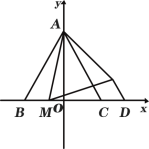
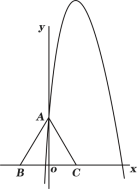
【题目】如图1,在平面直角坐标系中,等边△ABC的边BC在x轴上,A(0,3),B(![]() ,0),点M(
,0),点M(![]() ,0)为x轴上的一个动点,连接AM,将AM绕点A逆时针旋转60°得到AN.
,0)为x轴上的一个动点,连接AM,将AM绕点A逆时针旋转60°得到AN.
(1)当M点在B点的左方时,连接CN,求证:△BAM≌△CAN;
(2)如图2,当M点在边BC上时,过点N作ND//AC交x轴于点D,连接MN,若![]() ,试求D点的坐标;
,试求D点的坐标;
(3)如图3,是否存在点M,使得点N恰好在抛物线![]() 上,如果存在,请求出m的值,如果不存在,请说明理由.
上,如果存在,请求出m的值,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
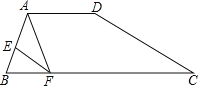
(1)求CF的长;
(2)若∠BFE=∠FAB,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
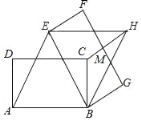
A. ![]() B. 2 C.
B. 2 C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
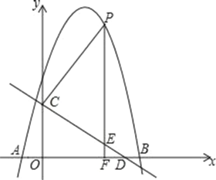
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以P、Q、C、D为顶点的四边形是平行四边形是否存在?若存在,请直接写出存在 个满足题意的点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com