
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
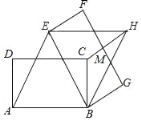
A. ![]() B. 2 C.
B. 2 C. ![]() D. 1
D. 1
【答案】A
【解析】
由旋转的性质得到AB=BE, 根据菱形的性质得到AE=AB, 推出△ABE是等边三角形,得到AB=6, AD=![]() , 根据三角函数的定义得到∠BAC=
, 根据三角函数的定义得到∠BAC=![]() , 求得AC⊥BE,推出C在对角线AH上,得到A, C, H共线,于是得到结论.
, 求得AC⊥BE,推出C在对角线AH上,得到A, C, H共线,于是得到结论.
解:如图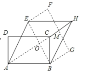
连接AC交BE与O点,
![]() 将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,
将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,
![]() AB=BE,
AB=BE,
![]() 四边形AEHB为菱形,
四边形AEHB为菱形,
![]() AE=AB,
AE=AB,![]() AB=AE=BE,
AB=AE=BE,
![]() △ABE 是等边三角形,
△ABE 是等边三角形,
![]() AB=6,AD=
AB=6,AD=![]() ,
,
![]() tan ∠CAB=
tan ∠CAB=![]()
![]() ∠BAC=
∠BAC=![]() ,
,
![]() AC⊥BE,
AC⊥BE,
![]() C在对角线AH上,
C在对角线AH上,![]() A, C, H共线,
A, C, H共线,
![]() AO=OH=
AO=OH=![]()
![]() OC=
OC=![]() BC=
BC=![]() .
.
![]() ∠COB=∠OBG=∠G=
∠COB=∠OBG=∠G=![]() ,
,
![]() 四边形OBGM是矩形,
四边形OBGM是矩形,
![]() OM=BG=BC=
OM=BG=BC=![]() ,
,
![]() HM=OH-OM=
HM=OH-OM=![]()
故选A.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
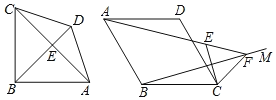
【题目】问题背景:如图1,在四边形ABCD中,∠ABC=90°,AB=CB=DB,DB⊥AC.
①直接写出∠ADC的大小;
②求证:AB2+BC2=AC2.
迁移应用:如图2,在四边形ABCD中,∠BAD=60°,AB=BC=CD=DA=2,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
①求证:△CEF是等边三角形;
②若∠BAF=45°,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西省地处中纬度,属于温带大陆性气候,因此适合种植玉米、高粱、大豆、花生等农作物,农民李大叔有一块总面积为![]() 的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
的长方形种植地,为了便于农作物之间互传花粉,提高产量,计划分垄种植玉米和高粱(每垄种植一种农作物)共32垄,种植的每种农作物的垄数不低于14垄,又不超过18垄(垄数为正整数),它们的占地面积、产量、利润分别如下:


农作物 | 占地面积( | 产量(千克/垄) | 利润(元/千克) |
玉米 | 30 | 60 | 0.5 |
高粱 | 20 | 50 | 0.8 |
(1)若设高粱种植了![]() 垄,请说明共有几种种植方案,分别是哪几种;
垄,请说明共有几种种植方案,分别是哪几种;
(2)在以上种植方案中,哪种方案获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中.
中.
![]() 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离![]() 的长
的长![]() 等于PC的长;
等于PC的长;
![]() 利用尺规作图,作出
利用尺规作图,作出![]() 中的线段PD.
中的线段PD.
![]() 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
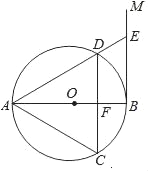
【题目】如图,AB是⊙O的直径,过点B作BM⊥AB,弦CD∥BM,交AB于点F,且DA=DC,连接AC,AD,延长AD交BM于点E.
(1)求证:△ACD是等边三角形;
(2)若AC=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com