
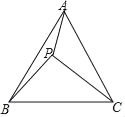
【题目】如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点F.AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.
∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,连EP,且延长BP,作AF⊥BP于点F.如图,
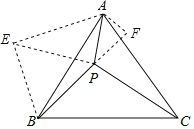
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
∴∠APF=30°,
∴在直角△APF中,AF=![]() AP=
AP=![]() ,PF=
,PF=![]() AP=
AP=![]() .
.
∴在直角△ABF中,AB2=BF2+AF2=(4+![]() )2+(
)2+(![]() )2=25+12
)2=25+12![]() .
.
则△ABC的面积是![]() AB2=
AB2=![]() (25+12
(25+12![]() )=9+
)=9+![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】我校开展了“图书节”活动,为了解开展情况,从七年级随机抽取了150名学生对他们每天阅读时间和阅读方式(要求每位学生只能选一种阅读方式)进行了问卷调查,并绘制了如下不完全的统计图
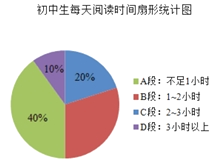
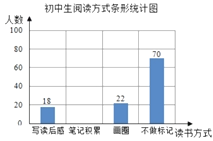
根据上述统计图提供的信息,解答下列问题:
(1)学生每天阅读时间人数最多的是______段,阅读时间在![]() 段的扇形的圆心角度数是______;
段的扇形的圆心角度数是______;
(2)补全条形统计图;
(3)若将写读后感、笔记积累、画圆点读三种方式为有记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年12月,旗团委号召各校组织开展捐赠衣物的“暖冬行动”![]() 某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
某校七年级六个班参加了这次捐赠活动,若每班捐赠衣物以100件为基准,超过的件数用正数表示,不足的件数用负数表示,记录如下:
班级 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
人数 | 40 | 43 | 45 | 44 | 40 | 38 |
件数 |
|
|
|
|
|
|
![]() 捐赠衣物最多的班比最少的班多多少件?
捐赠衣物最多的班比最少的班多多少件?
![]() 该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
该校七年级学生共捐赠多少件衣物?该校七年级学生平均每人捐赠多少件衣物?
查看答案和解析>>
科目:初中数学 来源: 题型:
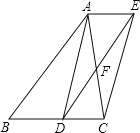
【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求回答问题:
(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.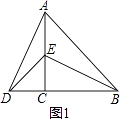
填空:线段AD,BE之间的关系为
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.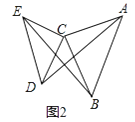
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.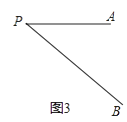
查看答案和解析>>
科目:初中数学 来源: 题型:
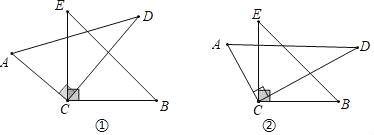
【题目】将一副分别含有30°和45°角的两个三角板的直角顶点C叠放在一起.
①如图,CD平分∠ECB,求∠ACB与∠DCE的和.
②如图,若CD不平分∠ECB,请你直接写出∠ACB与∠DCE之间所具有的数量关系(不要求说出理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )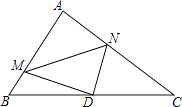
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com