
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.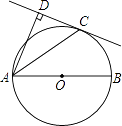
【答案】证明:连结OC,如图, 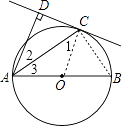
∵CD为⊙O的切线,
∴OC⊥AD,
∵AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠3,
∴∠2=∠3,
∴AC平分∠DAB.
【解析】连结OC,根据切线的性质得OC⊥AD,然后根据同一平面内垂直于同一直线的两条直线互相平行得出OC∥AD,故∠1=∠2,再根据等边对等角得出∠1=∠3,所以∠2=∠3。
【考点精析】掌握平行线的判定与性质和切线的性质定理是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.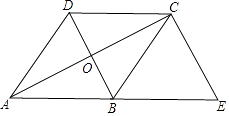
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4 ![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+5与坐标轴的交点B,C.已知D(0,3).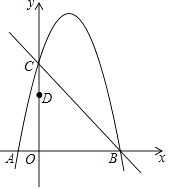
(1)求抛物线的解析式;
(2)M,N分别是BC,x轴上的动点,求△DMN周长最小时点M,N的坐标,并写出周长的最小值;
(3)连接BD,设M是平面上一点,将△BOD绕点M顺时针旋转90°后得到△B1O1D1 , 点B,O,D的对应点分别是B1 , O1 , D1 , 若△B1O1D1的两个顶点恰好落在抛物线上,请直接写出点O1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)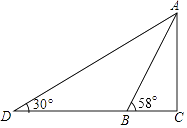
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机老姚某天上午营运全是在东西走向的解放路上进行.如 果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
+8,+6,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+8,﹣9,﹣12.
(1)将第几名乘客送到目的地时,老姚刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老姚距上午出发点多远?在出发点的东面 还是西面?
(3)若汽车耗油量为0.075L/km,这天上午老姚的出租车耗油多少L?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)判断下列未知数的值是不是方程2x2+x-1=0的根.
x1=-1,x2=1,x3=![]() .
.
(2)已知m是方程x2-x-2=0的一个根,求代数式m2-m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com