
【题目】如图,抛物线y=﹣x2+bx+c经过直线y=﹣x+5与坐标轴的交点B,C.已知D(0,3).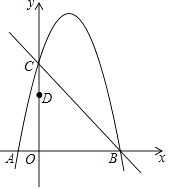
(1)求抛物线的解析式;
(2)M,N分别是BC,x轴上的动点,求△DMN周长最小时点M,N的坐标,并写出周长的最小值;
(3)连接BD,设M是平面上一点,将△BOD绕点M顺时针旋转90°后得到△B1O1D1 , 点B,O,D的对应点分别是B1 , O1 , D1 , 若△B1O1D1的两个顶点恰好落在抛物线上,请直接写出点O1的坐标.
【答案】
(1)解:由题意C(0,5),B(5,0),
把C(0,5),B(5,0)的坐标代入y=﹣x2+bx+c得到 ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+4x+5.
(2)解:如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.
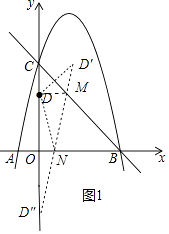
易知D′(2,5),D″(0,﹣3),
设直线D′D″的解析式为y=kx+b,则有 ![]() ,
,
解得 ![]() ,
,
∴y=4x﹣3,
∴N( ![]() ,0),
,0),
由 ![]() ,解得
,解得 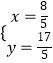 ,
,
∴M( ![]() ,
, ![]() ),
),
∴△DMN周长最小时点M( ![]() ,
, ![]() ),N(
),N( ![]() ,0),
,0),
△DMN的周长的最小值=D′D″= ![]() =2
=2 ![]() .
.
(3)解:①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).
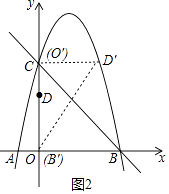
②如图3中,点B′、D′在抛物线上时,设点B′(x,﹣x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,﹣x2+4x+10).
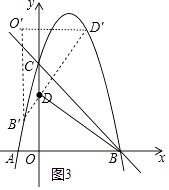
把D′坐标代入y=﹣x2+4x+5中,得到﹣x2+4x+10=﹣(x+3)2+4(x+3)+5,
解得x=﹣ ![]() ,
,
∴B′(﹣ ![]() ,
, ![]() ),
),
∴O′(﹣ ![]() ,
, ![]() ),
),
综上所述,满足条件的点O′的坐标为(0,5)或(﹣ ![]() ,
, ![]() ).
).
【解析】(1)求出B、C两点坐标,利用待定系数法即可解决问题;(2)如图1中,作点D关于BC的对称点D′,点D关于x轴的对称点D″,连接D′D″交BC于M,交x轴于N,连接DM,DN.此时△DMN的周长最小.求出D′、D″的坐标,直线D′D″的解析式即可解决问题;(3)分两种情形①如图2中,当O′和D′在抛物线上时,易知点O′与点C重合,CD′=OD=3,此时O′(0,5).②如图3中,点B′、D′在抛物线上时,设点B′(x,﹣x2+4x+5)的横坐标为x+1,则点D′的坐标为(x+3,﹣x2+4x+10).把D′的坐标代入抛物线的解析式,求出x即可解决问题;
【考点精析】掌握二次函数的性质是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )
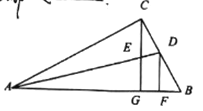
A. ①②④ B. ②③④ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
(1)请用两种不同方法,求图2中阴影部分的面积(不用化简)
方法1:____________________
方法2:____________________
(2)观察图2,写出![]() ,
,![]() ,
,![]() 之间的等量关系,并验证;
之间的等量关系,并验证;

(3)根据(2)题中的等量关系,解决如下问题:
①若![]() ,
,![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
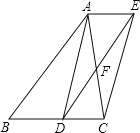
【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.
(x>0)的图象与一次函数y=3x的图象相交于点A,其横坐标为2.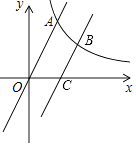
(1)求k的值;
(2)点B为此反比例函数图象上一点,其纵坐标为3.过点B作CB∥OA,交x轴于点C,直接写出线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果A,B都是由几个不同整数构成的集合,由属于A又属于B的所有整数构成的集合叫做A,B的交集,记作A∩B.例如:若A={1,2,3},B={3,4,5},则A∩B={3};若A={0,﹣62,37,2},B={2,﹣1,37,﹣5,0,19},则A∩B={37,0,2}.
(1)已知C={4,3},D={4,5,6},则C∩D={ };
(2)已知E={1,m,2},F={6,7},且E∩F={m},则m= ;
(3)已知P={2m+1,2m﹣1},Q={n,n+2,n+4},且P∩Q={m,n},如果关于x的不等式组![]() ,恰好有2019个整数解,求a的取值范围.
,恰好有2019个整数解,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
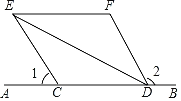
【题目】已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com