
【题目】(1)判断下列未知数的值是不是方程2x2+x-1=0的根.
x1=-1,x2=1,x3=![]() .
.
(2)已知m是方程x2-x-2=0的一个根,求代数式m2-m的值.
【答案】(1)x1=-1和x3=![]() 是方程的根;(2)2.
是方程的根;(2)2.
【解析】
(1)利用方程解的定义找到相等关系.即将未知数分别代入方程式看是否成立.
(2)一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值;即用这个数代替未知数所得式子仍然成立;将m代入原方程即可求m2-m的值.
解:(1)当x1=-1时,2x2+x-1=2-1-1=0,所以x1=-11是方程2x2+x-1=0的解;
当x2=1时, 2x2+x-1=2+1-1=2,所以x2=1不是方程2x2+x-1=0的解;
当x3=![]() .时,2x2+x-1=
.时,2x2+x-1=![]() +
+![]() -1=0,所以x3=
-1=0,所以x3=![]() .是方程2x2+x-1=0的解.
.是方程2x2+x-1=0的解.
(2)把x=m代入方程x2-x-2=0可得:m2-m-2=0,
即m2-m=2,
故m2-m的值为2.


科目:初中数学 来源: 题型:
【题目】如图,池塘边有一块长为18m,宽为10m的长方形土地,现在将其 余三面留出宽都是xm的小路,中间余下的长方形部分做菜地,用整式表示:
(1)菜地的长a= m,宽b= m;
(2)菜地面积S= m2;
(3)当x=0.5m时,菜地面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )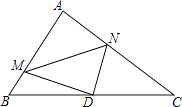
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C、D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)求证:CE∥DF;
(2)若∠DCE=126°,求∠DEF的度数.
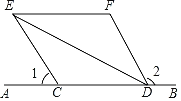
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 . 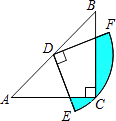
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y= ![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题: 
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点A的坐标为(0,1),取一点B(b,0),连接AB,做线段AB的垂直平分线l1 , 过点B作x轴的垂线l2 , 记l1 , l2的交点为P.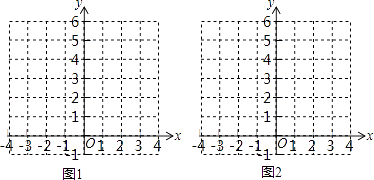
(1)当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹);
(2)小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来发现:这些点P竟然在一条曲线L上!
①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线;
②设点P到x轴,y轴的距离分别是d1 , d2 , 求d1+d2的范围,当d1+d2=8时,求点P的坐标;
③将曲线L在直线y=2下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线y=kx+3与这条“W”形状的新曲线有4个交点,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com