
【题目】我校开展了“图书节”活动,为了解开展情况,从七年级随机抽取了150名学生对他们每天阅读时间和阅读方式(要求每位学生只能选一种阅读方式)进行了问卷调查,并绘制了如下不完全的统计图
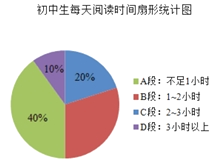
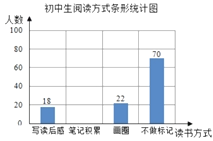
根据上述统计图提供的信息,解答下列问题:
(1)学生每天阅读时间人数最多的是______段,阅读时间在![]() 段的扇形的圆心角度数是______;
段的扇形的圆心角度数是______;
(2)补全条形统计图;
(3)若将写读后感、笔记积累、画圆点读三种方式为有记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
【答案】(1)A,108°;(2)见解析;(3)![]()
【解析】
(1)求出阅读时间在![]() 段的所占百分比即可得到学生每天阅读时间人数最多的是A段;用360°乘以阅读时间在
段的所占百分比即可得到学生每天阅读时间人数最多的是A段;用360°乘以阅读时间在![]() 段的所占百分比即可得到对应的扇形的圆心角度数;
段的所占百分比即可得到对应的扇形的圆心角度数;
(2)根据总人数求出读书方式为“笔记积累”的学生数,即可补全条形统计图;
(3)用笔记积累人数除以有记忆阅读的人数即可得解.
解:(1)阅读时间在![]() 段的所占百分比为:
段的所占百分比为:![]() ,
,
∴学生每天阅读时间人数最多的是A段;
阅读时间在![]() 段的扇形的圆心角度数是:
段的扇形的圆心角度数是:![]() ;
;
故答案为:A,108°;
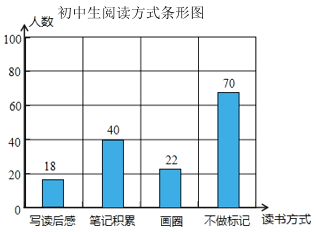
(2)读书方式为“笔记积累”的学生数为:150-18-22-70=40(人),
补全条形统计图如图:
(3)![]() ,
,
答:笔记积累人数占有记忆阅读人数的![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
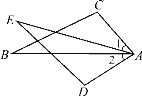
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE均为等边三角形,且点B,C,D在同一直线上,连结AD,BE,分别交CE和AC于点G,H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由;
(3)试猜想△CGH是什么特殊的三角形,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
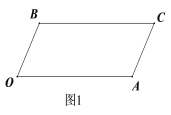
【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
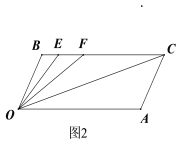
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
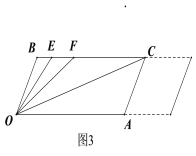
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明乘坐家门口的公共汽车前往西安北站去乘高铁,在行驶了三分之一路程时,小明估计继续乘公共汽车到北站时高铁将正好开出,于是小明下车改乘出租车,车速提高了一倍,结果赶在高铁开车前半小时到达西安北站.已知公共汽车的平均速度是20千米/小时(假设公共汽车及出租车保持匀速行使,途中换乘、红绿灯等待等情况忽略不计),请回答以下两个问题:
(1)出租车的速度为_____千米/小时;
(2)小明家到西安北站有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
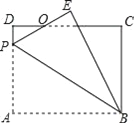
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com