
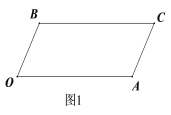
【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
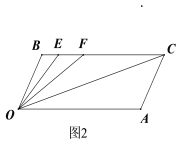
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
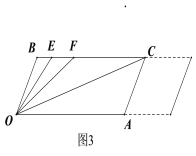
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
【答案】(1) 答案见详解,(2) 答案见详解,(3) 答案见详解,(4) 答案见详解.
【解析】
(1)由同旁内角互补,两直线平行证明.
(2)由∠FOC=∠AOC,并且OE平分∠BOF得到∠EOC=∠EOF+∠FOC=![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)=![]() ∠BOA,算出结果.
∠BOA,算出结果.
(3)先得出结论:∠OCB:∠OFB的值不发生变化,理由为:由BC与AO平行,得到一对内错角相等,由∠FOC=∠AOC,等量代换得到一对角相等,再利用外角性质等量代换即可得证;
(4)设∠BOE=∠EOF=α,∠FOC=∠COA=β,根据外角的性质分别用α和β表示出∠OEB和∠OCA,由∠OEB=∠OCA,即可得出α=β=15°,求出∠OCA即可.
(1)∵BC∥OA,
∴∠B+∠O=180°,又∵∠B=∠A,
∴∠A+∠O=180°,
∴OB∥AC;
(2)∵∠B+∠BOA=180°,∠B=120°,
∴∠BOA=60°,
∵OE平分∠BOF,
∴∠BOE=∠EOF,又∵∠FOC=∠AOC,
∴∠EOC=∠EOF+∠FOC=![]() (∠BOF+∠FOA)
(∠BOF+∠FOA)
=![]() ∠BOA=30°;
∠BOA=30°;
(3)结论:∠OCB:∠OFB的值不发生变化.理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2;
(4)由(1)知:OB∥AC,
则∠OCA=∠BOC,
由(2)可以设:∠BOE=∠EOF=α,∠FOC=∠COA=β,
则∠OCA=∠BOC=2α+β,
∠OEB=∠EOC+∠ECO=α+β+β=α+2β,
∵∠OEB=∠OCA,
∴2α+β=α+2β,
∴α=β,
∵∠AOB=60°,
∴α=β=15°,
∴∠OCA=2α+β=30°+15°=45°.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣ ![]()
(x<0)交于点P(﹣1,n),且F是PE的中点.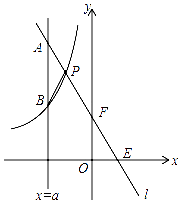
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),
①当a为何值时,△ABP是以点P为直角顶点的直角三角形?
②当a为何值时,PA=PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题; 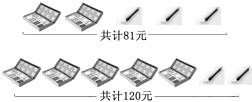
(1)求出每个颜料盒,每支水笔各多少元?
(2)若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?
(3)恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.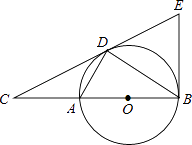
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ,
,
![]() ,
,
![]() ,
,
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校开展了“图书节”活动,为了解开展情况,从七年级随机抽取了150名学生对他们每天阅读时间和阅读方式(要求每位学生只能选一种阅读方式)进行了问卷调查,并绘制了如下不完全的统计图
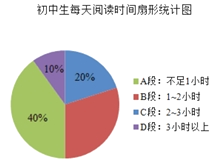
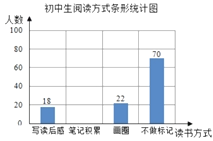
根据上述统计图提供的信息,解答下列问题:
(1)学生每天阅读时间人数最多的是______段,阅读时间在![]() 段的扇形的圆心角度数是______;
段的扇形的圆心角度数是______;
(2)补全条形统计图;
(3)若将写读后感、笔记积累、画圆点读三种方式为有记忆阅读,求笔记积累人数占有记忆阅读人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED=
,∠BAC的平分线交BC于D,过点C作CG⊥AB于G,交AD于E,过点D作DF⊥AB于F.下列结论①∠CED= ![]() ;②
;②![]() ;③∠ADF=
;③∠ADF= ![]() ;④CE=DF.正确的是( )
;④CE=DF.正确的是( )
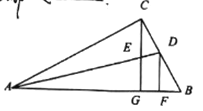
A. ①②④ B. ②③④ C. ①③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
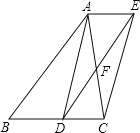
【题目】如图,已知点D是△ABC的边BC的中点,直线AE∥BC,过点D作直线DE∥AB,分别交AE、AC于点E、F。
(1)求证:四边形ADCE是平行四边形;
(2)如果四边形ADCE是矩形,△ABC应满足什么条件?并说明理由;
(3)如果四边形ADCE是菱形,直接写出△ABC应满足的条件是 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com