
����Ŀ��ijУΪ����������չ����л�ͬѧ����ʦ��������һЩˮ�ʺ����Ϻ���Ϊ��Ʒ���������ͼ����������Ϣ������������⣻ 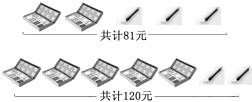
��1�����ÿ�����ϺУ�ÿ֧ˮ�ʸ�����Ԫ��
��2����ѧУ�ƻ��������Ϻк�ˮ�ʹ�20�������÷��ò�����340Ԫ�������Ϻ��������ٸ���
��3��ǡ���̵�����Żݴ����������취���£����Ϻа������Żݣ�ˮ��10֧���ϳ������ְ������Żݣ���ѧУ��������ͬ��������ͬһ��Ʒ�����Ҹý�Ʒ����������10������������������������Ϻк��㻹�ǹ���ˮ�ʺ��㣮
���𰸡�
��1���⣺��ÿ�����Ϻ�ΪxԪ��ÿ֧ˮ��ΪyԪ��
��������ã� ![]() ��
��
��� ![]() ��
��
��ÿ�����Ϻ�Ϊ18Ԫ��ÿ֧ˮ��Ϊ15Ԫ��
��2���⣺�蹺�����Ϻ�a������ˮ��Ϊ20��a����������ã�
18a+15��20��a����340��
���a��13 ![]() ��
��
�������Ϻ������13����
��3���⣺�蹺�������Ϊm������m��10��
������֪���������Ϻ�y1����m�ĺ�����ϵʽ��y1=18��70%m��
��y1=12.6m��
����ˮ��y2=15��10+15����m��10����80%��
��y2=30+12m��
��y1=y2ʱ����12m+30=12.6mʱ�����m=50��
��y1��y2ʱ����12.6m��12m+30ʱ�����m��50��
��y1��y2ʱ����12.6m��12m+30ʱ�����m��50��
����������������Ʒ����10��������50��ʱ�������Ϻк��㣮
������Ʒ����50��ʱ����ˮ�ʺ����Ϻ�Ǯ����ͬ��
����������1����ÿ�����Ϻ�ΪxԪ��ÿ֧ˮ��ΪyԪ��Ȼ���г���������⼴�ɣ���2���蹺�����Ϻ�a������ˮ��Ϊ20��a�����������÷��ò�����340Ԫ�г�����ʽ������⣻��3���蹺�������Ϊm�����г���������ʽ�������������ʽ�������Ʒ������Ȼ��д���������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ���dz������е����꼶ѧ��������4����ȫһ�������ǰ壨��ͼ1��ƴ����һ���dz�������ͼ�Σ���ͼ2���������ʦ�Ժ��֪����ͼ����һ�������Σ�����������ı���Ҳ��һ�������Σ�Ϊ������һ����̽����С�������ǰ�����߳���![]() ��ʾ����ͼ3���������������ηֱ���������ABCD��������EFGH��ʾ��Ȼ���������ֲ��õķ���������������ABCD�������
��ʾ����ͼ3���������������ηֱ���������ABCD��������EFGH��ʾ��Ȼ���������ֲ��õķ���������������ABCD�������
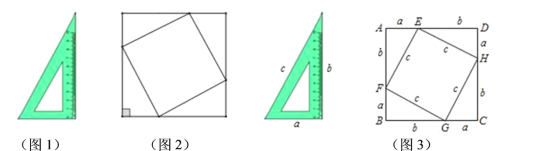
��1�����������ֲ�ͬ�ķ��������������ABCD�������
����һ�� ��
�������� ��
��2�����ݣ�1���ļ����������ܵõ���ô���Ľ��ۣ�
��3��������������������2���еĽ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ƽ���ȫ������ѧ�����������˶�����ʵʩ����֯���ͬѧ��չ�������ϵĵڶ����û������ij��ѧ���齨�������ţ�����������ë��ƹ�����赸���š����������š��������ţ�Ϊ�˽���Уѧ������4�����Ż��ϲ���������У�����ȡ���ֳ����������ˡ�����ϲ���ĸ����š����飬����������ݻ��Ƴ����²�������ͳ�Ʊ��������ͼ���е���Ϣ����������⣺
������� | ���� | ռ���������� |
���� | 60 | m |
�赸 | 30 | 0.25 |
������ | n | 0.15 |
���� | 12 | 0.1 |

��1��������������������m��n��ֵ��
��2���벹ȫͳ��ͼ��
��3���������60��ϲ������ͬѧ����3����ϲ����������У��3000��ѧ��������Ƹ�У��ϲ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
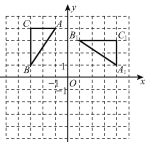
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC��������ֱ�ΪA(-1��4)��B(-3��1)��C(-3��4)����A1B1C1������ABC��ijһ����ת�õ���.
(1)��ֱ��д����ת���ĵ�������________����ת����_____����
(2)����ABCƽ�Ƶõ���A2B2C2��ʹ�õ�A2������Ϊ(0��-1)���뻭��ƽ�ƺ����A2B2C2�������ƽ�Ƶľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϸ�۲죬�ҹ���
���и�ͼ�е�MA1��NAnƽ�У�

��1��ͼ���еġ�A1+��A2= ______ �ȣ�
ͼ���еġ�A1+��A2+��A3= ______ �ȣ�
ͼ���еġ�A1+��A2+��A3+��A4= ______ �ȣ�
ͼ���еġ�A1+��A2+��A3+��A4+��A5= ______ �ȣ�
����
�ڢ��ͼ�еġ�A1+��A2+��A3+��+��A11= ______ ��
��2����n��ͼ�еġ�A1+��A2+��A3+��+��An+1= ______
��3������֤��ͼ�ڵĽ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0����y�ύ�ڵ�C��0��4����x�ύ�ڵ�A�͵�B�����е�A������Ϊ����2��0���������ߵĶԳ���x=1�������߽��ڵ�D����ֱ��BC���ڵ�E��
��1���������ߵĽ���ʽ��
��2������F��ֱ��BC�Ϸ����������ϵ�һ�����㣬�Ƿ���ڵ�F��ʹ�ı���ABFC�����Ϊ15�������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
��3��ƽ����DE��һ����ֱ��l��ֱ��BC�ཻ�ڵ�P�����������ཻ�ڵ�Q������D��E��P��QΪ������ı�����ƽ���ı��Σ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��m��6����B��n��1���ڷ���������ͼ���ϣ�AD��x���ڵ�D��BC��x���ڵ�C��DC=5��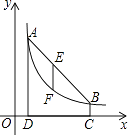
��1����m��n��ֵ��д�������������ı���ʽ��
��2������AB��E���߶�AB��һ�㣬����E��x��Ĵ��ߣ�������������ͼ���ڵ�F����EF= ![]() AD�������E�����꣮
AD�������E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
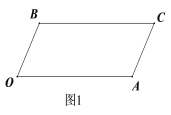
����Ŀ����ͼ1��ʾ����֪BC��OA, ��B=��A=120��.
��1��֤����OB��AC;
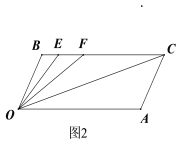
��2����ͼ2��ʾ������E,F��BC�ϣ��ҡ�FOC=��AOC,OEƽ�֡�BOF�����EOC�Ķ���.
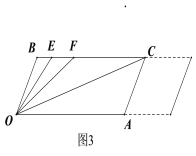
��3���ڣ�2���������£�������ƽ��AC����ͼ3��ʾ����ô��OCB�á�OFB�ı�ֵ�Ƿ���֮�����仯�����仯����˵�����ɣ������仯������������ֵ.
��4���ڣ�2���ͣ�3���������£�����OEB=��OCAʱ�����OCA�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AB�ӳ�����һ�㣬DΪ�߶�BC��һ�㣬CD��2BD��EΪ�߶�AC��һ�㣬CE��2AE
![]()
(1)��AB��18��BC��21����DE�ij���
(2)��AB��a����DE�ij���(�ú�a�Ĵ���ʽ��ʾ)
(3)��ͼ�������߶εij���֮�����߶�AD���ȵ�7������![]() ��ֵΪ�� ����
��ֵΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com