
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣ ![]()
(x<0)交于点P(﹣1,n),且F是PE的中点.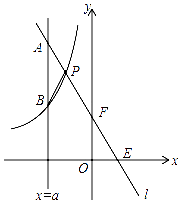
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),
①当a为何值时,△ABP是以点P为直角顶点的直角三角形?
②当a为何值时,PA=PB.
【答案】
(1)解:∵点P(﹣1,n)在反比例函数y=﹣ ![]() 图象上,
图象上,
∴n=4,
∴P(﹣1,4),
∵F是PE的中点,
∴F(0,2),
∴ ![]() ,
,
∴ ![]() ,
,
∴y=﹣2x+2
(2)解:①∵△ABP是以点P为直角顶点的直角三角形,
∴∠APB=90°=∠EOF,
∵直线AB∥y轴,
∴∠BAP=∠OFE,
∴△APB∽△FOE,
∴ ![]() =
= ![]()
当x=a时,y=﹣2a+2,
∴A(a,﹣2a+2),
∵P(﹣1,4),
∴AP= ![]() =
= ![]() =
= ![]() |a+1|
|a+1|
当x=a时,y=﹣ ![]() ,
,
∴B(a,﹣ ![]() ),
),
∴AB=|﹣2a+2+ ![]() ,
,
∵直线EF的解析式为y=﹣2x+2,
∴E(1,0),F(0,2),
∴OF=2,EF= ![]() ,
,
∴ ![]() ,
,
∴a= ![]() (舍)或a=﹣1(舍)或a=﹣8,
(舍)或a=﹣1(舍)或a=﹣8,
即:a=﹣8时,△ABP是以点P为直角顶点的直角三角形;
②如图,
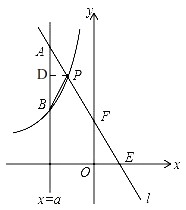
过P作PD⊥AB,垂足为点D,
∵P(﹣1,4),
∴D点的纵坐标为4,
∵PA=PB,
∴点D为AB的中点,
由题意知,A点的纵坐标为﹣2a+2,B点的纵坐标为 ![]() ,
,
∴ ![]() ,
,
解得a1=﹣2,a2=﹣1(舍去).
∴当a=﹣2时,PA=PB
【解析】(1)将点P(﹣1,n)在代入反比例函数解析式可求得n的值,从而得到点P的坐标,然后再求得点F的坐标,接下来,利用待定系数法求解即可;
(2)①先判断出△APB∽△FOE,然后依据相似三角形对应边成比例的性质列方出求解即可;②利用线段的中点坐标建立方程求解即可.
【考点精析】掌握反比例函数的性质是解答本题的根本,需要知道性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
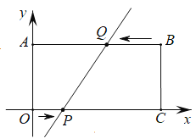
【题目】如图,在平面直角坐标系中,长方形OABC的边OC、OA分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4),OC=8.
(1)直接写出点B、C的坐标;
(2)点P从原点O出发,在边OC上以每秒1个单位长度的速度匀速向C点移动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点移动,当一个点到达终点时,另一个点随之停止移动,设移动的时间为t秒钟,探究下列问题:
① 当t值为多少时,直线PQ∥y轴?
② 在整个运动过程中,能否使得四边形BCPQ的面积是长方形OABC的面积的![]() ?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形,为了作进一步的探究,小明将三角板的三边长用![]() 表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
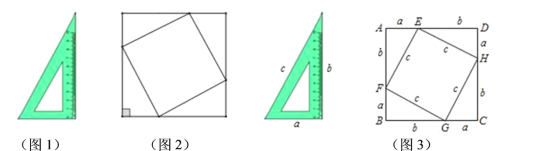
(1)请你用两种不同的方法计算出正方形ABCD的面积;
方法一: .
方法二: .
(2)根据(1)的计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.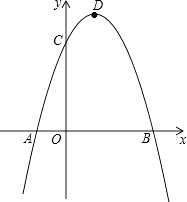
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副分别含有30°和45°角的两个直角三角板,拼成如图所示,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( ) 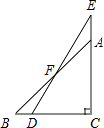
A.10°
B.15°
C.25°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
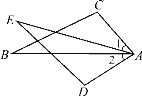
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
社团类别 | 人数 | 占总人数比例 |
球类 | 60 | m |
舞蹈 | 30 | 0.25 |
健美操 | n | 0.15 |
武术 | 12 | 0.1 |

(1)求样本容量及表格中m、n的值;
(2)请补全统计图;
(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
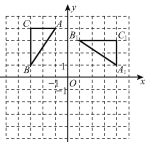
【题目】如图,在平面直角坐标系中,△ABC三个顶点分别为A(-1,4),B(-3,1),C(-3,4),△A1B1C1是由△ABC绕某一点旋转得到的.
(1)请直接写出旋转中心的坐标是________,旋转角是_____°;
(2)将△ABC平移得到△A2B2C2,使得点A2的坐标为(0,-1),请画出平移后的△A2B2C2,并求出平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
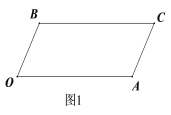
【题目】如图1所示,已知BC∥OA, ∠B=∠A=120°.
(1)证明:OB∥AC;
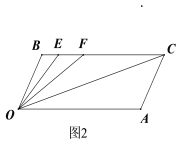
(2)如图2所示,若点E,F在BC上,且∠FOC=∠AOC,OE平分∠BOF,求∠EOC的度数.
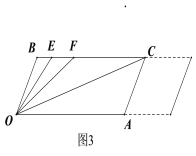
(3)在(2)的条件下,若左右平移AC,如图3所示,那么∠OCB∶∠OFB的比值是否随之发生变化?若变化,请说明理由;若不变化,请求出这个比值.
(4)在(2)和(3)的条件下,当∠OEB=∠OCA时,求∠OCA的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com