
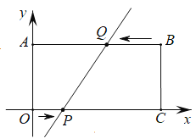
【题目】如图,在平面直角坐标系中,长方形OABC的边OC、OA分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4),OC=8.
(1)直接写出点B、C的坐标;
(2)点P从原点O出发,在边OC上以每秒1个单位长度的速度匀速向C点移动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点移动,当一个点到达终点时,另一个点随之停止移动,设移动的时间为t秒钟,探究下列问题:
① 当t值为多少时,直线PQ∥y轴?
② 在整个运动过程中,能否使得四边形BCPQ的面积是长方形OABC的面积的![]() ?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
【答案】(1)B(8,4)、C(8,0);(2)![]() 秒;(3)P(2,0),Q(4,4).
秒;(3)P(2,0),Q(4,4).
【解析】
(1)由点A的坐标是(0,4),OC=8即可得到结论.
(2)由OP=t,BQ=2t,得到AQ=8-2t ,P(t,0),Q(8-2t,4),由PQ∥y轴,得到t=8-2t ,解方程即可.
(3)由SBCPQ=![]() SOABC,列方程求解即可得到t的值,从而得到OP,AQ的值,即可得到结论.
SOABC,列方程求解即可得到t的值,从而得到OP,AQ的值,即可得到结论.
(1)由点A的坐标是(0,4),OC=8得:B(8,4)、C(8,0).
(2)由题意得:OP=t,BQ=2t,
∴AQ=8-2t ,
∴P(t,0),Q(8-2t,4).
∵PQ∥y轴,
∴t=8-2t ,
∴t=![]() ,
,
∴当t值为![]() (秒)时,直线PQ∥y轴.
(秒)时,直线PQ∥y轴.
(3)∵SBCPQ=![]() SOABC,∴
SOABC,∴![]() ,解得:t=2.
,解得:t=2.
当t=2时,OP=2,AQ=8-2t=4,∴P(2,0),Q(4,4).


科目:初中数学 来源: 题型:
【题目】为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数![]() 、
、![]() ,A、B两点之间的距离记作AB.
,A、B两点之间的距离记作AB.
当A、B两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=![]() =
=![]() .
.
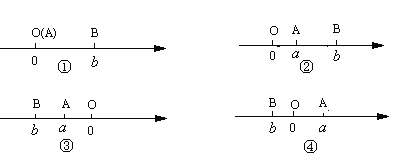
当A、B两点都不在原点时:
(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=![]() =
=![]() =
=![]()
回答下列问题:
(1)综上所述,数轴上A、B两点之间的距离AB= .
(2)数轴上表示2和-4的两点A和B之间的距离AB= .
(3)数轴上表示![]() 和-2的两点A和B之间的距离AB= ,如果AB=2,则
和-2的两点A和B之间的距离AB= ,如果AB=2,则![]() 的值为 .
的值为 .
(4)若代数式![]() 有最小值,则最小值为 .
有最小值,则最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为△ABC内一点,OD⊥AB于点D,OE⊥AC于点E,OF⊥BC于点F,若OD=OE=OF,连接OA,OB,OC,下列结论不一定正确的是( )
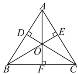
A. △BOD≌△BOF B. ∠OAD=∠OBF
C. ∠COE=∠COF D. AD=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自4月以来,我市推出了一项“共享单车”的便民举措,为人们的城市生活出行带来了方便.图(1)所示的是某款单车的实物图.图(2)是这辆单车的部分几何示意图,其中车支架BC的长为20cm,且∠CBA=75°,∠CAB=30°.求车架档AB的长.(参考数据:sin75°= ![]() ,cos75°=
,cos75°= ![]() ,tan75°=2+
,tan75°=2+ ![]() )
)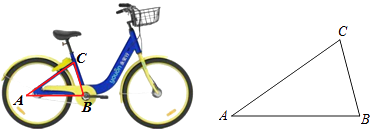
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
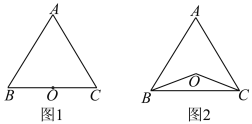
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC的内部,则∠ABC=∠ACB成立吗?并说明理由;
(3)若点O在△ABC的外部,则∠ABC=∠ACB成立吗?请画图表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣ ![]()
(x<0)交于点P(﹣1,n),且F是PE的中点.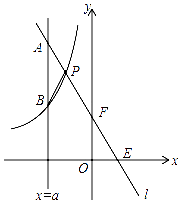
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),
①当a为何值时,△ABP是以点P为直角顶点的直角三角形?
②当a为何值时,PA=PB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com