
【题目】点A、B在数轴上分别表示实数![]() 、
、![]() ,A、B两点之间的距离记作AB.
,A、B两点之间的距离记作AB.
当A、B两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=![]() =
=![]() .
.
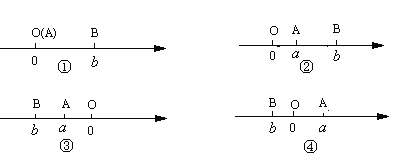
当A、B两点都不在原点时:
(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=![]() =
=![]() =
=![]()
回答下列问题:
(1)综上所述,数轴上A、B两点之间的距离AB= .
(2)数轴上表示2和-4的两点A和B之间的距离AB= .
(3)数轴上表示![]() 和-2的两点A和B之间的距离AB= ,如果AB=2,则
和-2的两点A和B之间的距离AB= ,如果AB=2,则![]() 的值为 .
的值为 .
(4)若代数式![]() 有最小值,则最小值为 .
有最小值,则最小值为 .
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-1,6)的“2属派生点”P′的坐标为_____________;
(2)若点P的“3属派生点”P′的坐标为(6,2),则点P的坐标___________;
(3)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
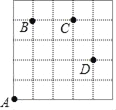
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、D在坐标轴上,其坐标分别为(2,0),(0,4),对角线AC⊥x轴. 
(1)求直线DC对应的函数解析式
(2)若反比例函数y= ![]() (k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
(k>0)的图象经过DC的中点M,请判断这个反比例函数的图象是否经过点B,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于 ![]() EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( )
EF的长为半径作弧,两弧交于点G;作射线AG,交边CD于点H.若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为( ) 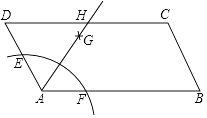
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查公司对本区域的共享单车数量及使用次数进行了调查发现,今年3月份第1周共有各类单车1000辆,第2周比第1周增加了10%,第3周比第2周增加了100辆.
调查还发现某款单车深受群众喜爱,第1周该单车的每辆平均使用次数是这一周所有单车平均使用次数的2.5倍,第2周、第3周该单车的每辆平均使用次数都比前一周增长一个相同的百分数m,第3周所有单车的每辆平均使用次数比第1周增加的百分数也是m,而且第3周该款单车(共100辆)的总使用次数占到所有单车总使用次数的四分之一(注:总使用次数=每辆平均使用次数×车辆数).
(1)求第3周该区域内各类共享单车的总数量;
(2)求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
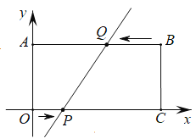
【题目】如图,在平面直角坐标系中,长方形OABC的边OC、OA分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4),OC=8.
(1)直接写出点B、C的坐标;
(2)点P从原点O出发,在边OC上以每秒1个单位长度的速度匀速向C点移动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点移动,当一个点到达终点时,另一个点随之停止移动,设移动的时间为t秒钟,探究下列问题:
① 当t值为多少时,直线PQ∥y轴?
② 在整个运动过程中,能否使得四边形BCPQ的面积是长方形OABC的面积的![]() ?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
?若能,请直接写出P、Q两点的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪是一名非常爱钻研的七年级学生,他将4块完全一样的三角板(如图1)拼成了一个非常工整的图形(如图2),请教老师以后得知:该图形是一个正方形,并且里面的四边形也是一个正方形,为了作进一步的探究,小明将三角板的三边长用![]() 表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
表示(如图3),将两个正方形分别用正方形ABCD和正方形EFGH表示,然后他用两种不用的方法计算了正方形ABCD的面积.
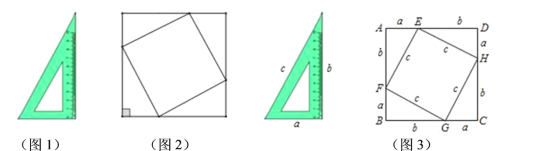
(1)请你用两种不同的方法计算出正方形ABCD的面积;
方法一: .
方法二: .
(2)根据(1)的计算结果,你能得到怎么样的结论?
(3)请用文字语言描述(2)中的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com