
【题目】阅读与理解:
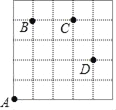
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
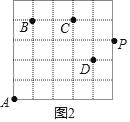
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
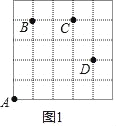
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
【答案】(1)A→C(+3,+4),B→C(+2,0),D→A(﹣4,﹣2)(2)标出P的位置见解析;(3)甲虫走过的总路程为16.
【解析】
(1)根据规定:向上、向右走为正,向下、向左走为负,结合图中点A、B、C、D的位置,即可得出结论;
(2) 根据坐标位置的确定规则,把从A处去到各处的行走路线逐一找出,如A→(+1,+4),即是从点A出发,往右移动2格,再往上移动4格,以此类推,最后找到点P的位置即可;
(3)根据点的运动路径,把经过的路线的长度相加,即各数对数值的绝对值相加即可得解.
解:(1)A→C向右3个单位,向上4个单位,
所以A→C(+3,+4),
同理:B→C(+2,0),D→A(﹣4,﹣2).
故答案是:A→C(+3,+4),B→C(+2,0),D→A(﹣4,﹣2)
(2)如图2所示.
(3)甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.


科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A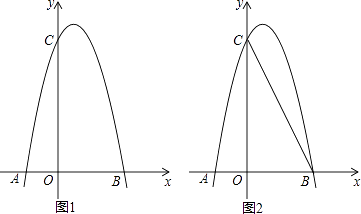
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F.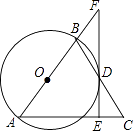
(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D. 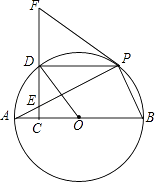
(1)证明:FP是⊙O的切线;
(2)若四边形OBPD是菱形,证明:FD=ED.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数![]() 、
、![]() ,A、B两点之间的距离记作AB.
,A、B两点之间的距离记作AB.
当A、B两点中有一点为原点时,不妨设A点在原点.如图①所示,则AB=OB=![]() =
=![]() .
.
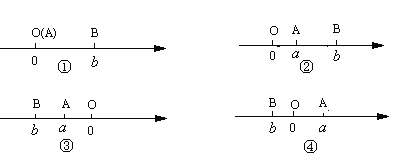
当A、B两点都不在原点时:
(1)如图②所示,点A、B都在原点的右边,不妨设点A在点B的左侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(2)如图③所示,点A、B都在原点的左边,不妨设点A在点B的右侧,则AB=OB-OA=![]() =
=![]() =
=![]() =
=![]()
(3)如图④所示,点A、B分别在原点的两边,不妨设点A在点O的右侧,则AB=OB+OA=![]() =
=![]() =
=![]()
回答下列问题:
(1)综上所述,数轴上A、B两点之间的距离AB= .
(2)数轴上表示2和-4的两点A和B之间的距离AB= .
(3)数轴上表示![]() 和-2的两点A和B之间的距离AB= ,如果AB=2,则
和-2的两点A和B之间的距离AB= ,如果AB=2,则![]() 的值为 .
的值为 .
(4)若代数式![]() 有最小值,则最小值为 .
有最小值,则最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在五一期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且余30个座位.
(1)求外出旅游的学生人数是多少,单租45座的客车需多少辆?
(2)已知45座的客车每辆租金250元,60座的客车每辆租金300元,为节省租金,并且保证每个学生都有座,决定同时租用两种客车,使得租车总数比单租45座的客车少一辆,问45座的客车和60座的客车分别租多少辆才能使得租金最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com