【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC=3，AB=5，则CE的长为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
根据三角形的内角和定理得出∠CAF+∠CFA=90°，∠FAD+∠AED=90°，根据角平分线和对顶角相等得出∠CEF=∠CFE，即可得出EC=FC，再利用相似三角形的判定与性质得出答案．
过点F作FG⊥AB于点G，
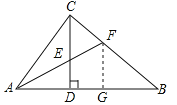
∵∠ACB=90°，CD⊥AB，∴∠CDA=90°，∴∠CAF+∠CFA=90°，∠FAD+∠AED=90°，∵AF平分∠CAB，∴∠CAF=∠FAD，∴∠CFA=∠AED=∠CEF，∴CE=CF，∵AF平分∠CAB，∠ACF=∠AGF=90°，∴FC=FG，∵∠B=∠B，∠FGB=∠ACB=90°，∴△BFG∽△BAC，∴
，∵AC=3，AB=5，∠ACB=90°，∴BC=4，∴
，∵FC=FG，∴
，解得：FC=
，即CE的长为．故选A．
53随堂测系列答案科目：初中数学 来源： 题型：
【题目】李师傅负责修理我校课桌椅，现知道李师傅修理2张课桌和3把椅子共需86分钟，修理5张课桌和2把椅子共需149分钟．
（1）请问李师傅修理1张课桌和1把椅子各需多少分钟
（2）现我校有12张课桌和14把椅子需要修理，要求1天做完，李师傅每天工作8小时，请问李师傅能在上班时间内修完吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于E交AB的延长线于点F．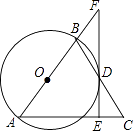
（1）求证：EF是⊙O的切线；
（2）若AE=6，FB=4，求⊙O的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图．AB是⊙O的直径，E为弦AP上一点，过点E作EC⊥AB于点C，延长CE至点F，连接FP，使∠FPE=∠FEP，CF交⊙O于点D．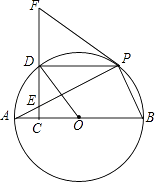 
（1）证明：FP是⊙O的切线；
（2）若四边形OBPD是菱形，证明：FD=ED．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点A、B在数轴上分别表示实数
、
，A、B两点之间的距离记作AB.
当A、B两点中有一点为原点时，不妨设A点在原点.如图①所示，则AB＝OB＝
＝
．
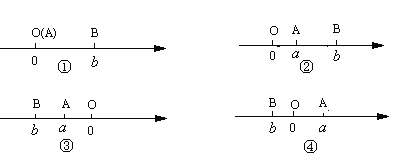
当A、B两点都不在原点时：
(1)如图②所示，点A、B都在原点的右边，不妨设点A在点B的左侧，则AB＝OB－OA＝
＝
＝
＝
(2)如图③所示，点A、B都在原点的左边，不妨设点A在点B的右侧，则AB＝OB－OA＝
＝
＝
＝
(3)如图④所示，点A、B分别在原点的两边，不妨设点A在点O的右侧，则AB＝OB＋OA＝
＝
＝
回答下列问题：
(1)综上所述，数轴上A、B两点之间的距离AB＝ ．
(2)数轴上表示2和－4的两点A和B之间的距离AB＝ ．
(3)数轴上表示
和－2的两点A和B之间的距离AB＝ ，如果AB＝2，则
的值为 ．
(4)若代数式
有最小值，则最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
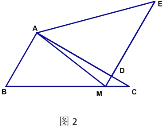
【题目】将一副三角板拼成如图所示的图形，即
，
，
，
，
与
相交于点
．
（1）如果
，那么
与
平行吗？试说明理由；
（2）将
绕着点
逆时针旋转，使得点
落在边上，联结
并延长交于点
，联结
，若
，
，
，求
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为△ABC内一点，OD⊥AB于点D，OE⊥AC于点E，OF⊥BC于点F，若OD＝OE＝OF，连接OA，OB，OC，下列结论不一定正确的是( )
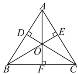
A. △BOD≌△BOF B. ∠OAD＝∠OBF
C. ∠COE＝∠COF D. AD＝AE
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△DCB中，∠A＝∠D＝72°，∠ACB＝∠DBC＝36°，则图中等腰三角形的个数是( )
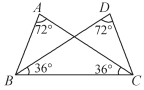
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
