
����Ŀ��С���������ſڵĹ�������ǰ��������վȥ�˸���������ʻ������֮һ·��ʱ��С�����Ƽ����˹�����������վʱ���������ÿ���������С���³��ij˳�������������һ����������ڸ�������ǰ��Сʱ����������վ����֪����������ƽ���ٶ���20ǧ��/Сʱ(���蹫���������������������ʹ��;�л��ˡ����̵Ƶȴ���������Բ���)����ش������������⣺
��1��������ٶ�Ϊ_____ǧ��/Сʱ��
��2��С���ҵ�������վ�ж���ǧ�ף�
���𰸡���1��40����2��С���ҵ�������վ�ľ���Ϊ30ǧ�ף�
��������
��1�����ݹ���������ƽ���ٶ���20ǧ��/Сʱ���ij˳�������������һ���ɵô𰸣�
��2��������ʻ����֮����·�̣��˳���ȳ˹����������ð�Сʱ�з�����⼴�ɣ�
�⣺��1��������ɵã�������ٶ�Ϊ40ǧ��/Сʱ��
�ʴ�Ϊ��40��
��2��С���ҵ�������վ�ľ���Ϊxǧ�ף�
������ã�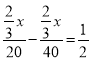 ����
����![]() ��
��
��ã�![]() ��
��
��С���ҵ�������վ�ľ���Ϊ30ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������CΪAB�ӳ�����һ�㣬����P�ӵ�A������AC������1cm/s���ٶ��˶���ͬʱ����Q�ӵ�C��������ͬ���ٶ���CA�����˶�������������ʱֹͣ�˶�������P��AB�Ĵ��ߣ��ֱ�O�ڵ�M�͵�N����֪��O�İ뾶Ϊ ![]() cm��AC=8cm�����˶�ʱ��Ϊt�룮
cm��AC=8cm�����˶�ʱ��Ϊt�룮 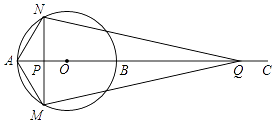
��1����֤��NQ=MQ��
��2����գ� �ٵ�t=ʱ���ı���AMQNΪ���Σ�
�ڵ�t=ʱ��NQ���O���У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����MON=30o����A1��A2��A3 ������ON�ϣ���B1��B2��B3������������OM�ϣ���A1B1A2. ��A2B2A3����A3B3A4������Ϊ�ȱ������Σ���OA1=l������A6B6A7 �ı߳�Ϊ�� ��

A��6 B��12 C��32 D��64
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��4��1����B��5��4�������߶�AB�Ƶ�A��ʱ����ת90����߶�AC�����C������Ϊ�� ��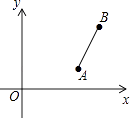
A.��1��2��
B.��2��1��
C.��7��0��
D.��1��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У��չ�ˡ�ͼ��ڡ����Ϊ�˽չ����������꼶�����ȡ��150��ѧ��������ÿ���Ķ�ʱ����Ķ���ʽ(Ҫ��ÿλѧ��ֻ��ѡһ���Ķ���ʽ)�������ʾ����飬�����������²���ȫ��ͳ��ͼ
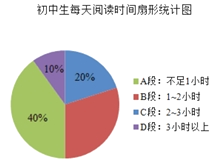
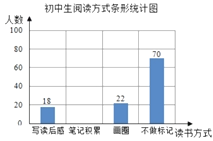
��������ͳ��ͼ�ṩ����Ϣ������������⣺
��1��ѧ��ÿ���Ķ�ʱ������������______�Σ��Ķ�ʱ����![]() �ε����ε�Բ�ĽǶ�����______��
�ε����ε�Բ�ĽǶ�����______��
��2����ȫ����ͳ��ͼ��
��3������д����С��ʼǻ��ۡ���Բ������ַ�ʽΪ�м����Ķ�����ʼǻ�������ռ�м����Ķ������İٷֱȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ݩ�1����1��4��2�����н��۲���ȷ���ǣ� ��
A.ƽ������1
B.�����ǩ�1
C.�����0.5
D.������3.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
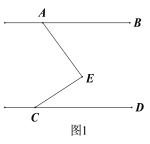
����Ŀ����ͼ����֪AB��CD,��E��ֱ��AB,CD֮��.
��1����֤����AEC=��BAE+��ECD;
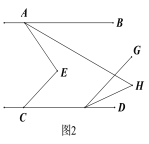
��2����AHƽ�֡�BAE�����߶�CE������CDƽ����FG.
����ͼ2������AEC=90����FHƽ�֡�DFG,���AHF�Ķ�����
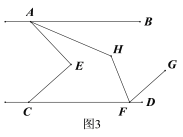
����ͼ3����FHƽ�֡�CFG,���жϡ�AHF���AEC��������ϵ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
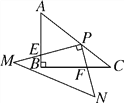
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬AB=3��BC=4.Rt��MPN�У���MPN=90�㣬��P��AC�ϣ�PM��AB�ڵ�E��PN��BC�ڵ�F����PE=2PFʱ��AP=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ��ش����⣺
��1�����ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=90�㣬B��C��D��һ��ֱ���ϣ�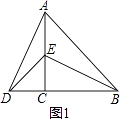
��գ��߶�AD��BE֮��Ĺ�ϵΪ
��2����չ̽��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬���ж�AD��BE�Ĺ�ϵ����˵�����ɣ�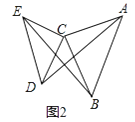
��3���������
��ͼ3���߶�PA=3����B���߶�PA��һ�㣬PB=5������AB����AB�Ƶ�A��ʱ����ת90��õ��߶�AC�����ŵ�B��λ�õı仯��ֱ��д��PC�ķ�Χ��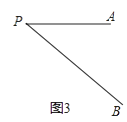
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com