
【题目】根据要求回答问题:
(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.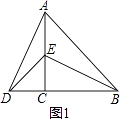
填空:线段AD,BE之间的关系为
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.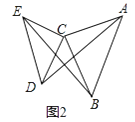
(3)解决问题
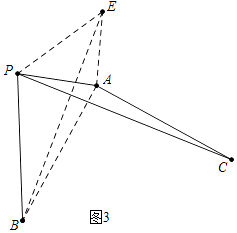
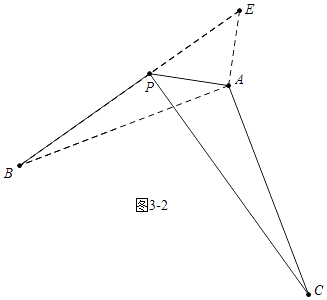
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.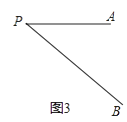
【答案】
(1)AD=BE,AD⊥BE
(2)解:结论:AD=BE,AD⊥BE.
理由:如图2中,设AD交BE于H,AD交BC于O.

∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,∠ACB=∠ECD=90°,
∴ACD=∠BCE,
在Rt△ACD和Rt△BCE中
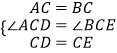 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE,
∵∠CAO+∠AOC=90°,∠AOC=∠BOH,
∴∠BOH+∠OBH=90°,
∴∠OHB=90°,
∴AD⊥BE,
∴AD=BE,AD⊥BE.
(3)解:如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,
∴PC=BE,
图3﹣1中,当P、E、B共线时,BE最小,最小值=PB﹣PE=5﹣3 ![]() ,
,
图3﹣2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+3 ![]() ,
,
∴5﹣3 ![]() ≤BE≤5+3
≤BE≤5+3 ![]() ,
,
即5﹣3 ![]() ≤PC≤5+3
≤PC≤5+3 ![]() .
.

【解析】解:(1)结论:AD=BE,AD⊥BE.
理由:如图1中,
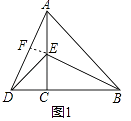
∵△ACB与△DCE均为等腰直角三角形,
∴AC=BC,CE=CD,
∠ACB=∠ACD=90°,
在Rt△ACD和Rt△BCE中
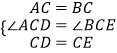 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠EBC=∠CAD
延长BE交AD于点F,
∵BC⊥AD,
∴∠EBC+∠CEB=90°,∵∠CEB=AEF,
∴∠EAD+∠AEF=90°,
∴∠AFE=90°,即AD⊥BE.
∴AD=BE,AD⊥BE.
所以答案是AD=BE,AD⊥BE.
【考点精析】根据题目的已知条件,利用全等三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明乘坐家门口的公共汽车前往西安北站去乘高铁,在行驶了三分之一路程时,小明估计继续乘公共汽车到北站时高铁将正好开出,于是小明下车改乘出租车,车速提高了一倍,结果赶在高铁开车前半小时到达西安北站.已知公共汽车的平均速度是20千米/小时(假设公共汽车及出租车保持匀速行使,途中换乘、红绿灯等待等情况忽略不计),请回答以下两个问题:
(1)出租车的速度为_____千米/小时;
(2)小明家到西安北站有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题: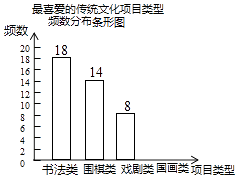
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店去年3至8月销售吐鲁番葡萄、哈密瓜的情况如下表:
3月 | 4月 | 5月 | 6月 | 7月 | 8月 | |
吐鲁番葡萄(单位:百公斤) | 4 | 8 | 5 | 8 | 10 | 13 |
哈密瓜(单位:百公斤) | 8 | 7 | 9 | 7 | 10 | 7 |
(1)请你根据以上数据填写下表:
平均数/百公斤 | 方差 | |
吐鲁番葡萄 | 8 | 9 |
哈密瓜 |
(2)请你根据上述信息,对这两种水果在去年3月份至8月份的销售情况进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
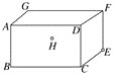
A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
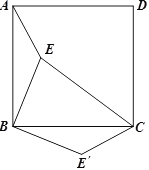
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一组数据x1,x2,…,xn的平均数为a,数据y1,y2,…,yn的平均数为b,则数据4x1+y1,4x2+y2,…,4xn+yn的平均数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com