
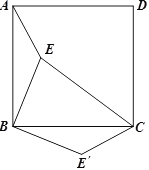
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,求EE′的长?并求出∠BE′C的度数?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
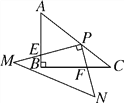
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求回答问题:
(1)问题发现
如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.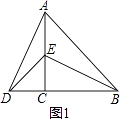
填空:线段AD,BE之间的关系为
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.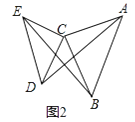
(3)解决问题
如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.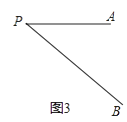
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生的大课间活动,准备购进一批跳绳,已知2根短绳和1根长绳共需56元,1根短绳和2根长绳共需82元.
(1)求每根短绳和每根长绳的售价各是多少元?
(2)学校准备购进这两种跳绳共50根,并且短绳的数量不超过长绳数量的2倍,总费用不超过1020元,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
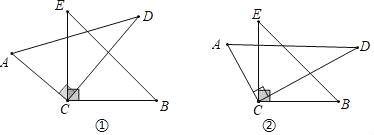
【题目】将一副分别含有30°和45°角的两个三角板的直角顶点C叠放在一起.
①如图,CD平分∠ECB,求∠ACB与∠DCE的和.
②如图,若CD不平分∠ECB,请你直接写出∠ACB与∠DCE之间所具有的数量关系(不要求说出理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
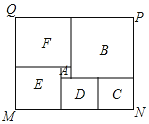
【题目】在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
![]() 若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
![]() 观察图形的特点可知,长方形相对的两边是相等的
观察图形的特点可知,长方形相对的两边是相等的![]() 如图中的MN和
如图中的MN和![]() 请根据这个等量关系,求出x的值;
请根据这个等量关系,求出x的值;
![]() 现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成
现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成![]() 两队合作施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
两队合作施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小洋八年级下学期的数学成绩(单位:分)如下表所示:
测试 类别 | 平时 | 期中 考试 | 期末 考试 | |||
测验1 | 测验2 | 测验3 | 测验4 | |||
成绩 | 106 | 102 | 115 | 109 | 112 | 110 |
(1)计算小洋该学期的数学平时平均成绩;
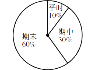
(2)如果该学期的总评成绩是根据如图所示的权重计算的,请计算出小洋该学期的数学总评成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
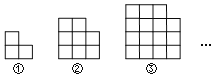
【题目】如图,是用大小相同的小正方形拼成的图形,拼第1个图需要3个小正方形,拼第2个图需要8个小正方形,拼第3个图需要15个小正方形,![]() .
.
![]() 根据拼图规律回答:第4个图形需要多少个小正方形;第n个图形比第
根据拼图规律回答:第4个图形需要多少个小正方形;第n个图形比第![]() 个图多需要多少个小正方形;第n个图形共需要多少个小正方形;
个图多需要多少个小正方形;第n个图形共需要多少个小正方形;
![]() 若第n个图形比第
若第n个图形比第![]() 个多2019个小正方形,求n.
个多2019个小正方形,求n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com