
【题目】在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为 . 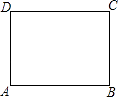
【答案】![]() 或
或 ![]()
【解析】解:①点A落在矩形对角线BD上,如图1,
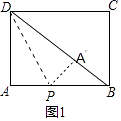
∵AB=4,BC=3,
∴BD=5,
根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,
∴BA′=2,
设AP=x,则BP=4﹣x,
∵BP2=BA′2+PA′2,
∴(4﹣x)2=x2+22,
解得:x= ![]() ,
,
∴AP= ![]() ;
;
②点A落在矩形对角线AC上,如图2,
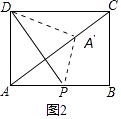
根据折叠的性质可知DP⊥AC,
∴△DAP∽△ABC,
∴ ![]() =
= ![]() ,
,
∴AP= ![]() =
= ![]() .
.
故答案为: ![]() 或
或 ![]() .
.
①点A落在矩形对角线BD上,如图1,由勾股定理得出BD=5,由根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,故BA′=2,设AP=x,则BP=4﹣x,根据勾股定理得出关于x的方程求解即可;②点A落在矩形对角线AC上,根据折叠的性质可知DP⊥AC从而判断出△DAP∽△ABC,根据相似三角形的性质得出AP的长度即可。


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4)与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)求抛物线的解析式;
(2)若点F事直线BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为15?若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为______.
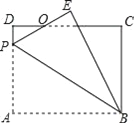
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB延长线上一点,D为线段BC上一点,CD=2BD,E为线段AC上一点,CE=2AE
![]()
(1)若AB=18,BC=21,求DE的长;
(2)若AB=a,求DE的长;(用含a的代数式表示)
(3)若图中所有线段的长度之和是线段AD长度的7倍,则![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题: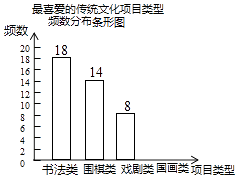
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线AC,BD相交于点O,延长AB至点E,使BE=AB,连接CE.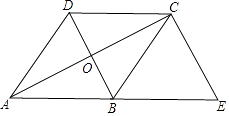
(1)求证:四边形BECD是平行四边形;
(2)若∠E=60°,AC=4 ![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机老姚某天上午营运全是在东西走向的解放路上进行.如 果规定向东为正,向西为负,他这天上午行车里程(单位:km)如下:
+8,+6,﹣10,﹣3,+6,﹣5,﹣2,﹣7,+4,+8,﹣9,﹣12.
(1)将第几名乘客送到目的地时,老姚刚好回到上午出发点?
(2)将最后一名乘客送到目的地时,老姚距上午出发点多远?在出发点的东面 还是西面?
(3)若汽车耗油量为0.075L/km,这天上午老姚的出租车耗油多少L?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com