【题目】如图，在
中．
利用尺规作图，在BC边上求作一点P，使得点P到AB的距离
的长
等于PC的长；
利用尺规作图，作出中的线段PD．
要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑
【答案】
作图见解析； （2）作图见解析.
【解析】
由点P到AB的距离
的长
等于PC的长知点P在
平分线上，再根据角平分线的尺规作图即可得（以点A为圆心，以任意长为半径画弧，与AC、AB分别交于一点，然后分别以这两点为圆心，以大于这两点距离的一半长为半径画弧，两弧交于一点，过点A及这个交点作射线交BC于点P，P即为要求的点）；
根据过直线外一点作已知直线的垂线的尺规作图即可得（以点P为圆心，以大于点P到AB的距离为半径画弧，与AB交于两点，分别以这两点为圆心，以大于这两点间距离一半长为半径画弧，两弧在AB的一侧交于一点，过这点以及点P作直线与AB交于点D，PD即为所求）．
如图，点P即为所求；
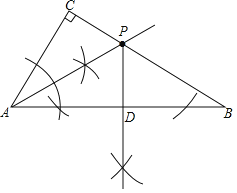
如图，线段PD即为所求．
天天练口算系列答案科目：初中数学 来源： 题型：
【题目】如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF．
（1）求证：AD平分∠BAC；
（2）直接写出AB+AC与AE之间的等量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们在学习“实数”时画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交数轴于点A”，请根据图形回答下列问题：
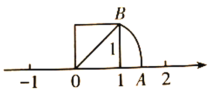
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=﹣
x2﹣
x+2与x轴交于A、B两点，与y轴交于点C
（1）求点A，B，C的坐标；
（2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；
（3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（6分）在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 68 | 109 | 136 | 345 | 368 | 701 |
摸到乒乓球的频率 | 0.68 | 0.73 | 0.68 | 0.69 | 0.70 | 0.70 |
（1）请估计：当n很大时，摸到白球的频率将会接近________；
（2）假如你去摸一次，你摸到白球的概率是_______，摸到黑球的概率是_______；
（3）试估算口袋中黑、白两种颜色的球各有多少只？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将半径为2，圆心角为120°的扇形OAB绕点A逆时针旋转60°，点O，B的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是( )
A. 
B. 2
－
C. 2－ D. 4－
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=2，求BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD的对角线相交于点O，AE平分∠BAD交BC于E， 若∠CAE=15°则∠BOE=（ ）
A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com