
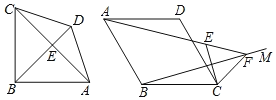
【题目】问题背景:如图1,在四边形ABCD中,∠ABC=90°,AB=CB=DB,DB⊥AC.
①直接写出∠ADC的大小;
②求证:AB2+BC2=AC2.
迁移应用:如图2,在四边形ABCD中,∠BAD=60°,AB=BC=CD=DA=2,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE、CF.
①求证:△CEF是等边三角形;
②若∠BAF=45°,求BF的长.
【答案】问题背景①∠ADC=135°;②证明见解析;迁移应用:①证明见解析;②BF=![]() .
.
【解析】
问题背景①利用等腰三角形的性质以及三角形的内角和定理即可解决问题.
②利用面积法解决问题即可.
迁移应用①如图2中,连BD,BE,DE.证明EF=FC,∠CEF=60![]() 即可解决问题.
即可解决问题.
②过B作BH⊥AE于H,设BH=AH=EH=x,利用面积法求解即可.
问题背景①∵BC=BD=BA,BD⊥AC,
∴∠CBD=∠ABD![]() ∠ABC=45°,
∠ABC=45°,
∴∠BCD=∠BDC![]() (180°﹣45°)=67.5°,∠BDA=∠BAD=67.5°,
(180°﹣45°)=67.5°,∠BDA=∠BAD=67.5°,
∴∠ADC=∠BDC+∠BDA=135°.
②如图1中,
设AB=BC=a,
∴S△ABC![]()
∵BE⊥AC,∠BCA=∠BAC=45°,
∴BE=AE=CE![]()
∵S△ABC![]() ,
,
∴![]() a2
a2![]() AC2
AC2
2a2=AC2,
∴AB2+BC2=AC2
迁移应用:①证明:如图2中,连BD,BE,DE.
∵AD=AB=BC=CD=2,
∴△ABD≌△BCD(SSS),
∴∠BAD=∠BCD
∵∠BAD=60°,
∴△ABD和△CBD为等边三角形
∵C沿BM对称得E点,
∴BM垂直平分CE,
∴设∠CBF=∠EBF=α,EF=CF,
∴∠BEC=90°﹣α,
∴∠ABE=120°﹣2α,
∴∠BAE=∠BEA=30°+α,
∴∠AEC=120°,
∴∠CEF=60°,
∴△CEF为等边三角形
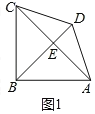
②解:易知∠BFH=30°
当∠BAF=45°时,
△ABE为等腰直角三角形
过B作BH⊥AE于H,
∴设BH=AH=EH=x,
∴S△ABE![]() 2xx=x2
2xx=x2
S△ABE![]() 2x=2,
2x=2,
∴x2=2,即x![]()
∵BF=2BH,
∴BF=2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为“厉行节能减排,倡导绿色出行”,某公司拟在我县甲、乙两个街道社区试点投放一批共享单车(俗称“小黄车”),这批自行车包括A、B两种不同款型,投放情况如下表:
成本单价 (单位:元) | 投放数量(单位:辆) | 总价(单位:元) | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合计(单位:元) | 7500 | ||
(1)根据表格填空:
本次试点投放的A、B型“小黄车”共有 辆;用含有![]() 的式子表示出B型自行车的成本总价为 ;
的式子表示出B型自行车的成本总价为 ;
(2)试求A、B两种款型自行车的单价各是多少元?
(3)经过试点投放调查,现在该公司决定采取如下方式投放A型“小黄车”:甲街区每100人投放n辆,乙街区每100人投放(n+2)辆,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有![]() 人,求甲街区每100人投放A型“小黄车”的数量.
人,求甲街区每100人投放A型“小黄车”的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a≠0)的图象如图所示,
(a≠0)的图象如图所示,
有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
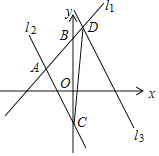
【题目】如图,直线l1:y=x+6与直线l2:y=kx+b相交于点A,直线l1与y轴相交于点B,直线l2与y轴负半轴相交于点C,OB=2OC,点A的纵坐标为3.
(1)求直线l2的解析式;
(2)将直线l2沿x轴正方向平移,记平移后的直线为l3,若直线l3与直线l1相交于点D,且点D的横坐标为1,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,AD=2![]() ,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM的长度为( )
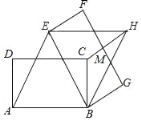
A. ![]() B. 2 C.
B. 2 C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com