
【题目】(12分)如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
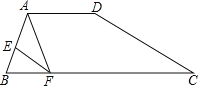
(1)求CF的长;
(2)若∠BFE=∠FAB,求AB的长.
【答案】(1)4;(2)![]() .
.
【解析】
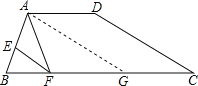
试题(1)作AG∥CD交BC于点G,根据平行四边形的性质可知CG=AD=2,由EF∥AG,AE=2EB,利用平行线分线段成比例定理可求出FG=2,CF=FG+GC即可求出结果;
(2)先证明△BFE∽△BAF,得到![]() ,由BE=
,由BE=![]() AB和BF=1可求出AB.
AB和BF=1可求出AB.
试题解析:解:(1)作AG∥CD交BC于点G,
∵AD∥BC,
∴四边形AGCD是平行四边形,
∴GC=AD,
∵AD=2,
∴GC=2,
∵BC=5,
∴BG=BC﹣GC=5﹣2=3,
∵EF∥DC,AG∥CD,
∴EF∥AG,
∴![]() ,
,
∴![]() ,
,
∵AE=2EB,
∴![]() ,
,
∴![]() ,
,
∵BG=3,
∴FG=2,
∴CF=FG+GC=2+2=4;
(2)∵∠BFE=∠FAB,∠B=∠B,
∴△BFE∽△BAF,
∴![]() ,
,
∴ABBE=BF2,
∴AB![]() AB=BF2,
AB=BF2,
∵BF=BC﹣FG=5﹣4=1,
∴AB=![]() .
.



科目:初中数学 来源: 题型:
【题目】为了解某市快递员的收入情况,现随机抽取了甲、乙两家快递公司50天的送货单,对两个公司的快递员人均每天的送货单数进行统计,数据如下:
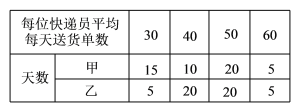
已知这两家快递公司的快递员的日工资方案 为:甲公司规定底薪70元,每单抽成1 元;乙公司规定底薪90元,每日前40单无抽成,超过40单的部分每单抽成3元.
(1)现从这50天中随机抽取1天,求这一天乙公司快递员人均送货单数超过40(不含40)单的概率;
(2)根据以上统计数据,若将各公司快递员的人均送货单数视为该公司各快递员的送货单数,
①估计甲快递公可各快递员的日均送货单数:
②小明拟到甲、乙两家快递公司中的一家应聘快递员的工作.如果仅从工资收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后郗进行了测试.现将项目选择情况及训练前后篮球定时定点投测试成绩整理作出如下统计图表.
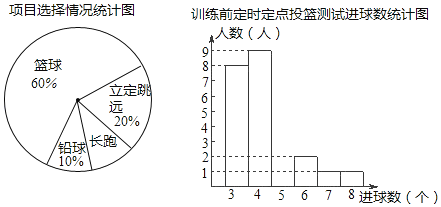
训练后篮球定时定点投篮测试进球数统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题
(1)送择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(2)直接补全“训练前篮球定时定点投测试进球数统计图”;
(3)若全区共有该年级学生4000人,请估计参加训练后篮球定时定点投篮进球数达到6个以上(包含6个)多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
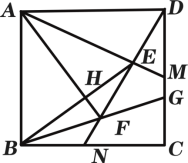
【题目】如图,在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,连接AM和DN交于点E,连接BE,作AH⊥BE于点H,延长AH与DN交于点F.连接BF并延长与CD交于点G,则MG的长度为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
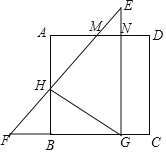
【题目】将正方形ABCD与等腰直角三角形EFG如图摆放,若点M、N刚好是AD的三等分点,下列结论正确的是( )
①△AMH≌△NME;②![]() ;③GH⊥EF;④S△EMN:S△EFG=1:16
;③GH⊥EF;④S△EMN:S△EFG=1:16
A.①②③④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 分别为x轴,y轴相交于A,B两点,点P(0,m)是y轴上一个动点,若以点P为圆心的圆P与x轴和直线l都相切,则m的值是_______.
分别为x轴,y轴相交于A,B两点,点P(0,m)是y轴上一个动点,若以点P为圆心的圆P与x轴和直线l都相切,则m的值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
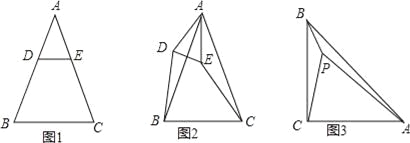
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() ,的图象和性质进行了探究探究过程如下,请补充完成:
,的图象和性质进行了探究探究过程如下,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.请直接写出m,n的值:m= ;n= .
x | … | ﹣2 | ﹣1 | 0 |
|
|
| n | 2 | 3 | 4 | … |
y | … |
| m | 0 | ﹣1 | ﹣3 | 5 | 3 | 2 |
|
| … |
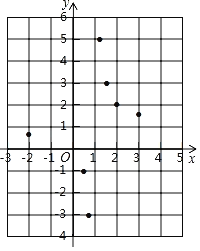
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)通过观察函数的图象,小明发现该函数图象与反比例函数y=![]() (k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,
(k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,![]() )是一组对称点,则其对称中心的坐标为 .
)是一组对称点,则其对称中心的坐标为 .
(5)当2≤x≤4时,关于x的方程kx+![]() =
=![]() 有实数解,求k的取值范围.
有实数解,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com