
����Ŀ����ͼ����Rt��ABC�У���A��90��AB��6��AC��8��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE�����˶�������P��PQ��BC��Q������Q��QR��BA��AC��R������Q���C�غ�ʱ����Pֹͣ�˶�����BQ��x��QR��y��
��1�����D��BC�ľ���DH�ij���
��2����y����x�ĺ�����ϵʽ����Ҫ��д�Ա�����ȡֵ��Χ����
��3���Ƿ���ڵ�P��ʹ��PQRΪ���������Σ������ڣ��������������Ҫ���x��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��![]() ��2��
��2��![]() ��3������
��3������
��������
�����������1��������RQC�ס�ABC���������������εĶ�Ӧ�߳ɱ��������DH��
��2�����������ε����Ʊ����y����x�ĺ�����ϵʽ��
��3������ͼ�Σ�����ͼ�ν������ۣ�
�� ��PQ=PRʱ������P��PM��QR��M����QM=RM��������1+��2=90������C+��2=90�������1=��C��
��cos��1=cosC=![]() =
=![]() ����
����![]() ���������x��ֵ��
���������x��ֵ��
�� ��PQ=RQʱ��-![]() x+6=
x+6=![]() ��x=6��
��x=6��
����PR=QRʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬��CR=![]() CE=
CE=![]() AC=2��
AC=2��
�����������1��![]()
![]() ��AB=6��AC=8��
��AB=6��AC=8��![]() ��
��
![]() ��DΪAB�е㣬
��DΪAB�е㣬![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ,
,
��2��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
��![]() ����
����![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��![]() ��
��
��3�����ڣ������������
����ͼ��1������![]() ʱ������P��
ʱ������P��![]() ��M����
��M����![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
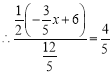 ��
��
![]() ��
��
����ͼ��2������![]() ʱ��
ʱ��

![]() ��
��
![]() ��
��
����ͼ��3������![]() ʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬
ʱ����RΪPQ�д����ϵĵ㣬���ǵ�RΪEC���е㣬
![]() ��
��
![]() ��
��
 ��
��
![]() ��
��
������������![]() Ϊ
Ϊ![]() ��6��
��6��![]() ʱ��
ʱ��![]() Ϊ���������Σ�
����������




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г��ȵ������߶�����β˳����ӹ��������ε����� ��
A. 4��2��2 B. 6��3��2 C. 5��3��9 D. 3��6��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��̨�ƣ�����Ϊ30Ԫ��ÿ����40Ԫ����ʱ��ƽ��ÿ��������600���������������һ�����ۼ۷�Χ�ڣ��ۼ�x��������y������ͼ�ĺ�����ϵ��
��1�����������y���ۼ�x�ĺ�����ϵʽ����д���Ա����ķ�Χ��
��2����ƽ��ÿ��������10000Ԫ�����ۼ�Ӧ��Ϊ����Ԫ��
��3����ÿ���µ���������Ϊw���Ƶ��ۼ۶�Ϊ����Ԫʱ��ÿ���¿��Ի���������������Ƕ���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������4���¼��������������ӣ���Ϊ����������������������Ϊ�����������������ˣ���Ϊ����������������������Ϊ��������Ȼ�¼��� �� �������¼��� �� �����¼���������ϼ��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��kx��b��k��0����ͼ��ƽ����ֱ��y��2x��3���ҽ�y���ڵ���0����1�������亯������ʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5�֣���2015����ɽ��ĩ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | 50 |
��1���뽫����������
��2���뽫����ͳ��ͼ����������
��3������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ��Ƕ��ٶȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
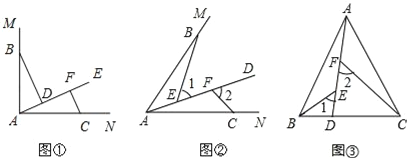
����Ŀ����1����ͼ1����MAN=90��������AE������ǵ��ڲ�����B��C�ֱ��ڡ�MAN�ı�AM��AN�ϣ���AB=AC��CF��AE�ڵ�F��BD��AE�ڵ�D����֤����ABD�ա�CAF��
��2����ͼ2����B��C�ֱ��ڡ�MAN�ı�AM��AN�ϣ���E��F���ڡ�MAN�ڲ�������AD�ϣ���1����2�ֱ�����ABE����CAF����ǣ���֪AB=AC���ҡ�1=��2=��BAC����֤����ABE�ա�CAF��
��3����ͼ3������ABC�У�AB=AC��AB��BC����D�ڱ�BC�ϣ�CD=2BD����E��F���߶�AD�ϣ���1=��2=��BAC������ABC�����Ϊ15������ACF����BDE�����֮�ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=x2��4��ͼ����y��Ľ��������ǣ� ��
A.��2��0��
B.����2��0��
C.��0��4��
D.��0����4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com