Question

【题目】如图，在四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E，F，求证：四边形AFCE是平行四边形．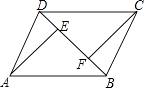

Answer 1

【答案】证明：连接AF、CE．

∵AE⊥BD，CF⊥BD，

∴∠AED=∠CFB=90°，AE∥CF，

∵BE=DF，

∴DE=BF，

在Rt△ADE后Rt△CBF中，

，

∴Rt△ADE≌Rt△CBF，

∴AE=CF，∵AE∥CF，

∴四边形AECF是平行四边形

【解析】要证四边形AECF是平行四边形，连接AF、CE．由已知AE⊥BD，CF⊥BD，可证得AE∥CF，再证明AE=CF，通过证Rt△ADE≌Rt△CBF即可。
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识，掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．